Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có: chọn ra 4 thầy cô từ 16 thầy cô có ![]() (cách chọn)
(cách chọn)
+ Để chọn được 4 giáo viên phải có cô giáo và đủ ba bộ môn, vậy có các trường hợp sau:
* Trường hợp 1: chọn 2 thầy toán, 1 cô lý, 1 cô hóa có ![]() (cách chọn)
(cách chọn)
* Trường hợp 2: chọn 1 thầy toán, 2 cô lý, 1 cô hóa có ![]() (cách chọn)
(cách chọn)
* Trường hợp 3: chọn 1 thầy toán, 1 cô lý, 2 cô hóa có ![]() (cách chọn)
(cách chọn)
Vậy xác suất để chọn được 4 người phải có cô giáo và có đủ ba bộ môn là
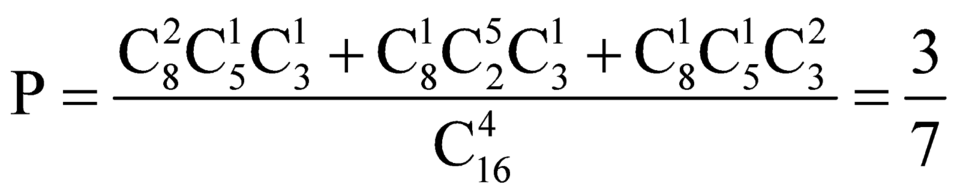

Chọn C
Gọi biến cố A: “2 giáo viên tập huấn gồm 1 thầy giáo và 1 cô giáo”.
Suy ra ![]() .
.
Vậy 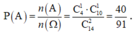 .
.

Chọn C.
Số phần tử của của không gian mẫu: ![]()
- Gọi A là biến cố: “Các giáo viên được chọn có 2 nam và 2 nữ”
![]()
![]()

Chọn C.
Số phần tử của của không gian mẫu: ![]()
- Gọi A là biến cố: “Các giáo viên được chọn có 2 nam và 2 nữ”
![]()
![]()

Số thành viên nữ của tố `23` là: `60. 5/12=25` (thành viên)
`=>` Số thành viên nam của tổ `23` là: `60-25=35` (thành viên)
`@TH1:` Chọn `3` giáo viên mà không có tổ trưởng
`=>` Có `C_25 ^2 .C_33^1 +C_25 ^1 .C_33^2=23100` cách
`@TH2:` Chọn `3` thành viên trong đó có `1` tổ trưởng là `1` trong `2` tổ trưởng nam.
`=>` Có `2.C_25 ^2=600` cách
`@TH3:` Chọn `3` thành viên trong đó có cả `2` tổ trưởng
`=>` Có `1.C_25 ^1=25` cách
`=>` Có tất cả `23100+600+25=23725` cách
`->bb B`

Đáp án A
Số cách chọn ngẫu nhiên 2 giáo viên từ 30 giáo viên là:![]()
Số cách chọn ngẫu nhiên 2 giáo viên khác trường là: ![]()
Xác suất chọn 2 giáo viên khác trường là:
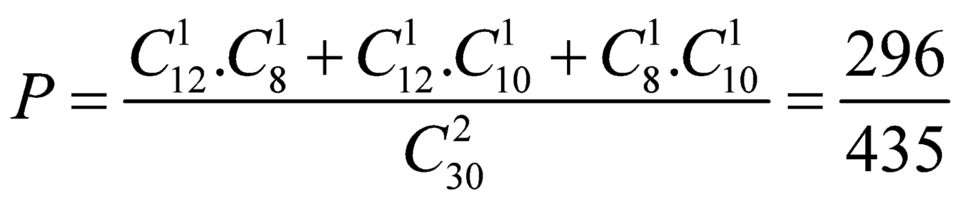

Coi 2 bạn nữ và cô giáo là 1 nhóm, kết hợp với 3 bạn nam ta được 4 "người"
Hoán vị 4 người trên bàn tròn: \(3!=6\) cách
Xếp cô giáo và 2 bạn nữ: \(2!=2\) cách
Tổng cộng: \(6.2=12\) cách

Cô Hoa ơi
Cố lên nhé
Nhất định cô sẽ đậu
Bọn em sẽ luôn ủng hộ cô
MK góp ý nha
Cô Hoa ơi !
Tự tin chiến thắng
Sáng tạo , tâm huyết
Kinh nghiệm chục năm
Chúc cô thi tốt
Cô Hoa kính yêu !
( Đây là lời của mink . Chúc cô của bạn thi tốt )