Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài này sử dụng định lý Mê-nê-la-uýt là ra nha. mình nói hướng làm
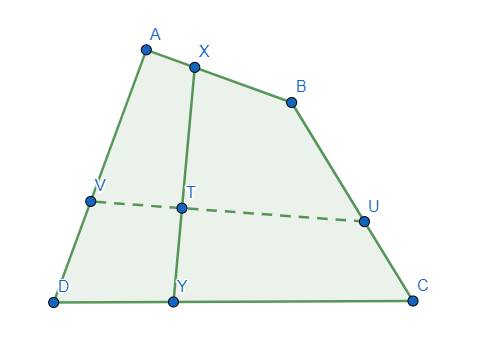
gọi Q là giao điểm của FG với BD. Ta chứng minh Q cố định bằng cách xác định tỉ số mà Q chia đoạn thẳng BD. Muốn xác định được tỉ số này ta cần bổ sung thêm H là giao điểm của đường tròn FG với đường thẳng AD (trường hợp đặc biệt là M trùng với điểm của cạnh CD, lúc đó FG với đường thẳng AD và ta dễ dàng xác định tỉ số cần tìm)
đặt độ dài cạnh hình thoi là a và đặt x=MD/MC. do tam giác MDE đồng dạng với tam giác MCB nên ta tính được DE=ax, AE=a(x+1), GA/GC=GE/GB=x+1
sử dụng định lý Mê-nê-la-uýt trong tam giác CDE với cát tuyến AF, ta có:
\(\frac{FC}{FE}\cdot\frac{AE}{AD}\cdot\frac{MD}{MC}=1\Rightarrow\frac{FC}{FE}\cdot\left(x+1\right)x=1\Rightarrow\frac{FC}{FE}=\frac{1}{x\left(x+1\right)}\)
áp dụng định lý Mê-nê-la-uýt trong tam giác ACE với cát tuyến GH ta có
\(\frac{HE}{HA}\cdot\frac{GA}{GC}\cdot\frac{FC}{FE}=1\Rightarrow\frac{HE}{HA}\left(x+1\right)\cdot\frac{1}{x\left(x+1\right)}=1\)
\(\Rightarrow\frac{HE}{HA}=x\Rightarrow\frac{HE}{HA-HE}=\frac{1}{1-x}\Rightarrow\frac{HE}{AE}=\frac{x}{1-x}\)
\(\Rightarrow HE=\widehat{CFN}=90^o-\widehat{FCI}\), suy ra:
\(\frac{HE}{HE+DE}=\frac{x+1}{\left(x+1\right)+\left(1-x\right)}\Rightarrow\frac{HE}{HD}=\frac{x+1}{2}\)
áp dụng định lý Mê-nê-la-uýt trong tam giác BDE với cát tuyến QH, ta có
\(\frac{QD}{QB}\cdot\frac{GB}{GE}\cdot\frac{HE}{HD}=1\Rightarrow\frac{QD}{QB}\cdot\frac{1}{x+1}\cdot\frac{x+1}{2}=1\)
như vậy Q chính là trọng tâm của tam giác ABC và đường thẳng FG luôn qua Q cố định

1.
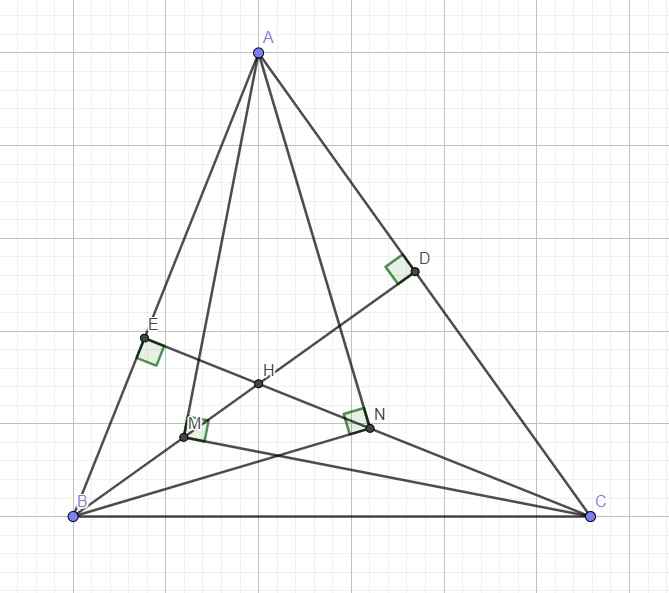
Tam giác AMC vuông tại M với đường cao MD
Áp dụng hệ thức lượng: \(AM^2=AD.AC\) (1)
Tương tự ta có:
\(AN^2=AE.AB\) (2)
Mặt khác xét hai tam giác vuông ABD và ACE có:
\(\widehat{BAC}\) chung
\(\Rightarrow\Delta_VABD\sim\Delta_VACE\) (g.g)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\) \(\Leftrightarrow AB.AE=AC.AD\) (3)
(1);(2);(3) \(\Rightarrow AM^2=AN^2\) \(\Rightarrow AM=AN\)
Bài 2 tham khảo tại đây:
Cho tam giác ABC vuông tại A , đường cao AH . Biết AB/AC = 20/21 , AH = 420 . Tính chu vi tam giác ABC - Hoc24