Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bổ đề: Cho tứ giác lồi bất kì thì tổng hai cạnh đối bé hơn tổng hai đường chéo (dễ chứng minh bằng cách sử dụng bất đẳng thức tam giác) (**)
Gọi E là giao điểm của AB và CD. Có thể xảy ra hai khả năng: ^B ≥ ^C hoặc ^B ≤ ^C
Giả sử ^B ≥ ^C (không mất tính tổng quát)
Trên tia đối của tia JA lấy K sao cho JA = JK
Dễ dàng có AD = BK (tứ giác ABKD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành)
IJ là đường trung bình của ∆ACK nên CK = 2IJ
Áp dụng bổ đề (**) vào tứ giác BCKD, ta được: BD + CK < CD + BK
Vậy BD + 2IJ < CD + AD (1)
Trong ∆ABC thì AC < AB + BC (2)
Cộng vế với vế (1) và (2), ta được: AC + BD + 2IJ < AB + BC + CD + DA

sao hả bạn bạn biết thì trả lời giúp mình còn ko thì đừng hỏi vớ vẩn nhé

A B C D O
Theo bất đẳng thức tam giác ta có:
OA + OB > AB
OB + OC > BC
OC + OD > CD
OD + OA > DA
Cộng 4 bđt trên theo vế ta được:
2(OA + OB + OC + OD) > AB + BC + CD + DA
<=> (OA + OC) + (OB + OD) > (AB + BC + CD + DA)/2
\(\Leftrightarrow AC+BD>\frac{AB+BC+CD+DA}{2}\)

Tứ giác có thể là hình vuông, chữ nhật phải không bạn?
P/s: Hỏi thôi chớ không trả lời đâu :D

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

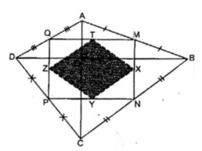
Trong △ ABD ta có:
M là trung điểm của AB
Q là trung điểm của AD nên MQ là đường trung bình của △ ABD.
⇒ MQ // BD và MQ = 1/2 BD (tính chất đường trung bình của tam giác) (1)
Trong △ CBD ta có:
N là trung điểm của BC
P là trung điểm của CD
nên NP là đường trung bình của △ CBD
⇒ NP // BD và NP = 1/2 BD (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: MQ // NP và MQ = NP nên tứ giác MNPQ là hình bình hành
AC ⊥ BD (gt)
MQ // BD
Suy ra: AC ⊥ MQ
Trong △ ABC có MN là đường trung bình ⇒ MN // AC
Suy ra: MN ⊥ MQ hay (NMQ) = 90 0
Vậy tứ giác MNPQ là hình chữ nhật.

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD