
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


5:
a: góc ACB=1/2*180=90 độ
Xét ΔAKH vuông tại K và ΔACB vuông tại A có
góc KAH chung
=>ΔAKH đồng dạng với ΔACB
b: Xét ΔADC và ΔBEC có
AD=BE
góc DAC=góc EBC
AC=BC
=>ΔADC=ΔBEC
=>DC=EC
=>ΔDEC cân tại C
góc CAB=45 độ
=>góc CDE=góc CAB=45 độ
=>ΔCDE vuông cân tại C


\(\sqrt{4x^2-4x+9}=3\\ \Rightarrow4x^2-4x+9=9\\ \Rightarrow4x\left(x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}4x=0\\x-1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Ta có: \(\sqrt{4x^2-4x+9}=3\)
\(\Leftrightarrow4x^2-4x=0\)
\(\Leftrightarrow4x\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)

Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}+\widehat{AOB}+\widehat{AMB}=360^0\)
=>\(\widehat{AMB}+100^0+90^0+90^0=360^0\)
=>\(\widehat{AMB}=80^0\)

\(\dfrac{\sqrt{3+2\sqrt{2}}+\sqrt{3-2\sqrt{2}}}{\sqrt{3+2\sqrt{2}}-\sqrt{3-2\sqrt{2}}}\)
\(=\dfrac{\sqrt{1+2\sqrt{2}+2}+\sqrt{2-2\sqrt{2}+1}}{\sqrt{1+2\sqrt{2}+2}-\sqrt{2-2\sqrt{2}+1}}\)
\(=\dfrac{\sqrt{\left(1+\sqrt{2}\right)^2}+\sqrt{\left(\sqrt{2}-1\right)^2}}{\sqrt{\left(1+\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{2}-1\right)^2}}\)
\(=\dfrac{\left|1+\sqrt{2}\right|+\left|\sqrt{2}-1\right|}{\left|1+\sqrt{2}\right|-\left|\sqrt{2}-1\right|}\)
\(=\dfrac{1+\sqrt{2}+\sqrt{2}-1}{1+\sqrt{2}-\left(\sqrt{2}-1\right)}\)
\(=\dfrac{2\sqrt{2}}{1+\sqrt{2}-\sqrt{2}+1}\)
\(=\dfrac{2\sqrt{2}}{2}=\sqrt{2}\)
Kết luận: ...


a, Thay tọa độ điểm ( 2;5 ) vào hàm số ta được ;
\(2\left(2m-1\right)+m-3=5\)
\(\Rightarrow m=2\)
b, - Gọi điểm cố định hàm số đi qua là M (x0; y0 ) ta được :
\(\left(2m-1\right)x_0+m-3=y_0\)
\(\Leftrightarrow2mx_0-x_0+m-3-y_0=0\)
\(\Leftrightarrow m\left(2x_0+1\right)-x_0-y_0-3=0\)
- Để hàm số luôn đi qua điểm cố định \(\Leftrightarrow\left\{{}\begin{matrix}2x_0+1=0\\x_0+y_0+3=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=-\dfrac{5}{2}\end{matrix}\right.\)
Vậy điểm cố định mà hàm số đi qua là : M ( -1/2; -5/2 )
c, - Thay điểm có hoành độ là \(\sqrt{2}-1\) vào hàm số ta được :
\(\left(\sqrt{2}-1\right)\left(2m-1\right)+m-3=0\)
\(\Leftrightarrow m=\dfrac{6+5\sqrt{2}}{7}\)
Vậy ...

3: Ta có: A=B|x-4|
\(\Leftrightarrow\dfrac{\sqrt{x}-2}{\sqrt{x}-5}:\dfrac{1}{\sqrt{x}-5}=\left|x-4\right|\)
\(\Leftrightarrow\left|x-4\right|=\sqrt{x}-2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=\sqrt{x}-2\left(x\ge4;x\ne25\right)\\x-4=2-\sqrt{x}\left(0< x< 4\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-\sqrt{x}-2=0\\x+\sqrt{x}-6=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(nhận\right)\\x=4\left(loại\right)\end{matrix}\right.\)
1: Thay x=9 vào A, ta được:
\(A=\dfrac{3-2}{3-5}=\dfrac{-1}{-2}=\dfrac{1}{2}\)
2: Ta có: \(B=\dfrac{3}{\sqrt{x}+5}+\dfrac{20-2\sqrt{x}}{x-25}\)
\(=\dfrac{3\sqrt{x}-15+20-2\sqrt{x}}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\)
\(=\dfrac{1}{\sqrt{x}-5}\)
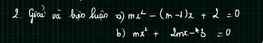






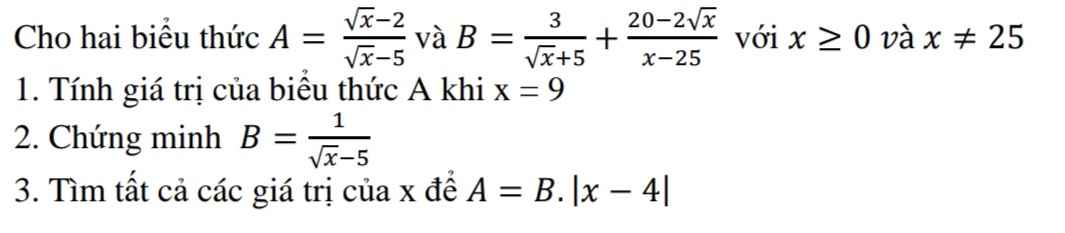
b: \(\text{Δ}=\left(2m\right)^2-4\cdot m\cdot\left(-3\right)=4m^2+12m\)
Để phương trinh vô nghiệm thì m(4m+12)<0
=>-3<m<0
Để phương trình có nghiệm kép thì m(4m+12)=0
=>m=0 hoặc m=-3
Để phương trình vô số nghiệm thì m(4m+12)>0
=>m>0 hoặc m<-3