
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a.\sqrt{0,01}-\sqrt{0,25}=\sqrt{0.1^2}-\sqrt{0,5^2}\)
\(=|0.1|-|0,5|=0,1-0,5=-0,4\)
\(\sqrt{0,01}-\sqrt{0,25}\)
\(=\sqrt{\frac{1}{100}}-\sqrt{\frac{25}{100}}\)
\(=\frac{1}{10}-\frac{5}{10}\)
\(=\frac{-2}{5}\)

a)\(3.\left(10:x\right)=111\)
\(\Rightarrow10:x=37\)
\(x=10:37\)
\(x=\frac{10}{37}\)
b)\(3.\left(10+x\right)=111\)
\(\Rightarrow10+x=37\)
\(x=37-10\)
\(x=27\)
c)\(3+\left(10.x\right)=111\)
\(\Rightarrow10x=108\)
\(x=108:10\)
\(x=\frac{54}{5}\)
d)\(3+\left(10+x\right)=111\)
\(\Rightarrow10+x=108\)
\(x=108-10\)
\(x=98\)


b)
\(\left(x+1\right)^2+3\)
ta có: \(\left(x+1\right)^2\) \(\geq\)0 với mọi x
=> \(\left(x+1\right)^2+3\) \(\geq\) \(3\) với mọi x
dấu bằng xảy ra<=>x+1=0
<=>x=1
vậy GTNN của biểu thức \(\left(x+1\right)^2+3\) là \(3\) <=> x= \(-1\)\

Gọi số HS mỗi lớp lần lượt là a,b,c,d
Ta có: \(\frac{a}{11}=\frac{b}{12}=\frac{c}{13}=\frac{d}{14}=\frac{a}{11}=\frac{2b}{24}=\frac{c}{13}=\frac{d}{14}=\frac{2b-a}{24-11}=\frac{39}{13}=3\)
\(\Rightarrow\frac{a}{11}=3\Rightarrow a=33;\frac{b}{12}=3\Rightarrow b=36;\frac{c}{13}=3\Rightarrow c=39;\frac{d}{14}=3\Rightarrow d=42\)
Vậy số HS 4 lớp lần lượt là 33;36;39;42(HS)


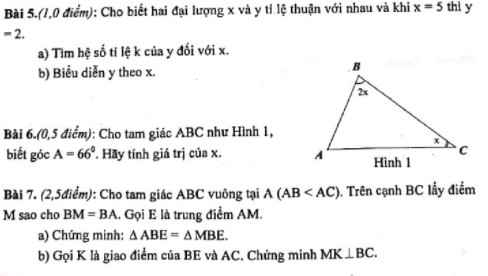
Bài 7:
a: Xét ΔABE và ΔMBE có
BA=BM
BE chung
EA=EM
Do đó: ΔABE=ΔMBE

a) \(14\dfrac{2}{5}\cdot\dfrac{7}{8}-6\dfrac{2}{5}\cdot\dfrac{7}{8}\)
\(=\dfrac{7}{8}\cdot\left(14\dfrac{2}{5}-6\dfrac{2}{5}\right)\)
\(=\dfrac{7}{8}\cdot\left(\dfrac{72}{5}-\dfrac{32}{5}\right)\)
\(=\dfrac{7}{8}\cdot\dfrac{40}{5}\)
\(=\dfrac{7}{8}\cdot8=7\)
b) \(\dfrac{1}{4}+\dfrac{3}{4}\cdot\dfrac{-5}{9}-\left(-\dfrac{2021}{2022}\right)^0\)
\(=\dfrac{3}{12}-\dfrac{5}{12}-1\)
\(=-\dfrac{2}{12}-\dfrac{12}{12}\)
\(=-\dfrac{14}{12}=-\dfrac{7}{6}\)
c) \(\dfrac{2}{3}\cdot\left(-6\right)+0,25:1\dfrac{1}{4}\)
\(=-4+\dfrac{1}{4}:\dfrac{5}{4}\)
\(=-4+\dfrac{1}{4}\cdot\dfrac{4}{5}\)
\(=\dfrac{-20}{5}+\dfrac{1}{5}=-\dfrac{19}{5}\)
d) \(\left(\left|-0,6\right|+\dfrac{4}{5}\right)\sqrt{\dfrac{9}{49}}+\left(\dfrac{-2}{5}\right)^3\)
\(=\left(0,6+\dfrac{4}{5}\right)\cdot\sqrt{\left(\dfrac{3}{7}\right)^2}+\dfrac{\left(-2\right)^3}{5^3}\)
\(=\dfrac{7}{5}\cdot\dfrac{3}{7}+\dfrac{-8}{125}\)
\(=\dfrac{3}{5}-\dfrac{8}{125}\)
\(=\dfrac{75}{125}-\dfrac{8}{125}=\dfrac{67}{125}\)
\(\text{#}Toru\)
\(a,14\dfrac{2}{5}.\dfrac{7}{8}-6\dfrac{2}{5}.\dfrac{7}{8}=\left(14\dfrac{2}{5}-6\dfrac{2}{5}\right).\dfrac{7}{8}=8.\dfrac{7}{8}=7\\ b,\dfrac{1}{4}+\dfrac{3}{4}.\dfrac{-5}{9}-\left(-\dfrac{2021}{2022}\right)^0\\ =\dfrac{1}{4}+\dfrac{-15}{36}-1\\ =\dfrac{1}{4}-\dfrac{5}{12}-1=\dfrac{3-5-12}{12}=-\dfrac{14}{12}=-\dfrac{7}{6}\)
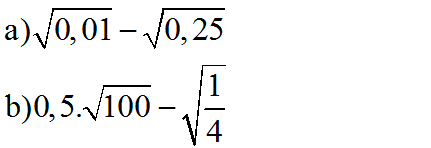

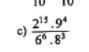 các bạn giúp mik giải đề cương vs nha . mong sự giúp đỡ của các bạn . bài nào bạn biết làm cx đ ko cần làm hết
các bạn giúp mik giải đề cương vs nha . mong sự giúp đỡ của các bạn . bài nào bạn biết làm cx đ ko cần làm hết 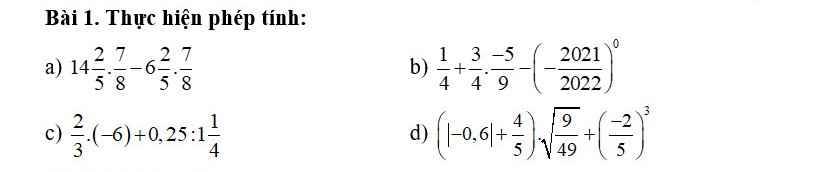 Mg giải giúp mình ạ
Mg giải giúp mình ạ
\(\left(x^2-16\right)\left(x^2-16\right)=0\)
\(\Rightarrow\left(x^2-16\right)=0\)
\(\Rightarrow x^2-16=0\)
\(\Rightarrow x^2=16\)
\(\Rightarrow\orbr{\begin{cases}x=4\\x=-4\end{cases}}\)