K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 5 2022
a: Xét ΔBDC có \(\widehat{BDC}>90^0\)
nên BC là cạnh lớn nhất
=>BC>BD
b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó;ΔABD=ΔEBD
c: Xét ΔABC có
AK là phân giác
BD là phân giác
AK cắt BD tại O
Do đó: O là tâm đường tròn nội tiếp ΔABC
=>CO là phân giác của góc ACB
Xét ΔOHC vuông tại H và ΔOKC vuông tại K có
CO chung
\(\widehat{HCO}=\widehat{KCO}\)
Do đó: ΔOHC=ΔOKC
Suy ra: OH=OK
MA
các bạn giải giúp m với ạ! Mình đang cần gấp bài 2 và bài 3II
0
9 tháng 1
\(M=\dfrac{3}{1+2}+\dfrac{3}{1+2+3}+...+\dfrac{3}{1+2+...+2022}\)
\(=\dfrac{3}{\dfrac{2\left(2+1\right)}{2}}+\dfrac{3}{\dfrac{3\left(3+1\right)}{2}}+...+\dfrac{3}{\dfrac{2022\left(2022+1\right)}{2}}\)
\(=\dfrac{6}{2\left(2+1\right)}+\dfrac{6}{3\left(3+1\right)}+...+\dfrac{6}{2022\cdot2023}\)
\(=\dfrac{6}{2\cdot3}+\dfrac{6}{3\cdot4}+...+\dfrac{6}{2022\cdot2023}\)
\(=6\left(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2022\cdot2023}\right)\)
\(=6\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2022}-\dfrac{1}{2023}\right)\)
\(=6\cdot\left(\dfrac{1}{2}-\dfrac{1}{2023}\right)=6\cdot\dfrac{2021}{4046}=\dfrac{12126}{4046}< 3\)
mà \(3< \dfrac{10}{3}\)
nên \(M< \dfrac{10}{3}\)
16 tháng 6 2020
tự kẻ hình nha
a) xét tam giác ACF và tam giác ABE có
góc A chung
AB=AC(gt)
AFC=AEB(=90 độ)
=> tam giác ACF= tam giác ABE(ch-gnh)
CF=BE(hai cạnh tương ứng)
b) từ tam giác ACF= tam giác ABE=> AF=AE(hai cạnh tương ứng)
xét tam giác AFH và tam giác AEH có
AF=AE(cmt)
AFH=AEH(=90 độ)
AH chung
=> tam giác AFH= tam giác AE(ch-cgv)
=> FH=EH( hai cạnh tương ứng)
=> tam giác FHE cân H
c) vì AF=AE=> tam giác AFE cân A=> AFE=AEF=180-FAE/2
vì tam giác ABC cân A=> ABC=ACB=180-BAC/2
=> AFE=ACB mà AFE đồng vị với ACB => EF//BC
d) từ tam giác AFH= tam giác AEH=> A1=A2( hai góc tương ứng)
đặt O là giao điểm của AH và EF
xét tam giác AFO và tam giác AEO có
AF=AE(cmt)
A1=A2(cmt)
AO chung
=> tam giác AFO=tam giác AEO (cgc)
=> AOF=AOC( hai góc tương ứng)
mà AOF+AOC=180 độ( kề bù)
=> AOF=AOC=180/2= 90 độ=> AH vuông góc với EF
M
29 tháng 11 2019
Bài giải
a, \(\frac{2}{7}x+\frac{1}{2}=-\frac{3}{4}\)
\(\frac{2}{7}x=-\frac{3}{4}-\frac{1}{2}\)
\(\frac{2}{7}x=-\frac{5}{4}\)
\(x=-\frac{5}{4}\text{ : }\frac{2}{7}\)
\(x=-\frac{35}{8}\)
b, \(\left(6x+\frac{2}{5}\right)=-\frac{8}{125}\)
\(6x=-\frac{8}{125}-\frac{2}{5}\)
\(6x=-\frac{58}{125}\)
\(x=-\frac{58}{125}\text{ : }6\)
\(x=\frac{-29}{375}\)
c, \(\left|x-\frac{2}{3}\right|\cdot\left(18-6x^2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}\left|x-\frac{2}{3}\right|=0\\18-6x^2=0\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x-\frac{2}{3}=0\\6x^2=18\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x=\frac{2}{3}\\x^2=3\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x=\frac{2}{3}\\x=\sqrt{3}\end{cases}}\)
\(\Rightarrow\text{ }x\in\left\{\frac{2}{3}\text{ ; }\sqrt{3}\right\}\)
NM
1
5 tháng 8 2021
a) Ta có: \(\widehat{BEC}\) là góc ngoài tại đỉnh E của ΔABE
nên \(\widehat{BEC}=\widehat{A}+\widehat{ABE}=90^0+\widehat{ABE}>90^0\)
hay \(\widehat{BEC}\) là góc tù
b) \(\widehat{BEA}=180^0-110^0=70^0\)
\(\Leftrightarrow\widehat{ABE}=20^0\)
\(\Leftrightarrow\widehat{ABC}=40^0\)
\(\Leftrightarrow\widehat{ACB}=50^0\)
24 tháng 4 2020
hết luôn bạn ạ nhưng nếu bạn giải được bài nào thì bạn cứ giải ạ
19 tháng 7 2021
a, \(2^3.2^5=2^8=256\)
\(\left(-3\right)^9:\left(-3\right)^5=\left(-3\right)^4=81\)
\(\left(-6\right)^9.6^5=\left(-1\right)^9.6^9.6^5=\left(-1\right).6^{14}\\ \left(\dfrac{1}{2}\right)^5=\dfrac{1}{32}\)
b, \(\left(\dfrac{3}{5}\right)^6.\left(\dfrac{5}{3}\right)^6=\left(\dfrac{3}{5}. \dfrac{5}{3}\right)^6=1^6=1\\ \left(-\dfrac{7}{8}\right)^9:\left(\dfrac{7}{4}\right)^9=\left(-\dfrac{7}{8}:\dfrac{7}{4}\right)^9=\left(-\dfrac{1}{2}\right)^9=-\dfrac{1}{512}\\ \left(\left(-\dfrac{1}{2}\right)^2\right)^3=\left(\dfrac{1}{2}\right)^{...}\Rightarrow\left(\dfrac{1}{64}\right)=\left(\dfrac{1}{2}\right)...\Rightarrow\left(\dfrac{1}{64}\right)=\left(\dfrac{1}{2}\right)^6\)
c, \(\left(\dfrac{2}{3}\right)^8=\left(\left(\dfrac{2}{3}\right)^4\right)^{...}\Rightarrow\left(\left(\dfrac{2}{3}\right)^4\right)^2=\left(\left(\dfrac{2}{3}\right)^4\right)^{...}\Rightarrow\left(\dfrac{2}{3}\right)^8=\left(\left(\dfrac{2}{3}\right)^4\right)^2\\ \left(\dfrac{1}{3}\right)^{12}:\left(-\dfrac{3}{9}\right)^{12}=\left(\dfrac{1}{3}.\left(-3\right)\right)^{12}=\left(-1\right)^{12}=1\\ \left(\dfrac{1}{3}\right)^{12}:\left(\dfrac{1}{3}\right)^{10}=\left(\dfrac{1}{3}\right)^2=\dfrac{1}{9}\)
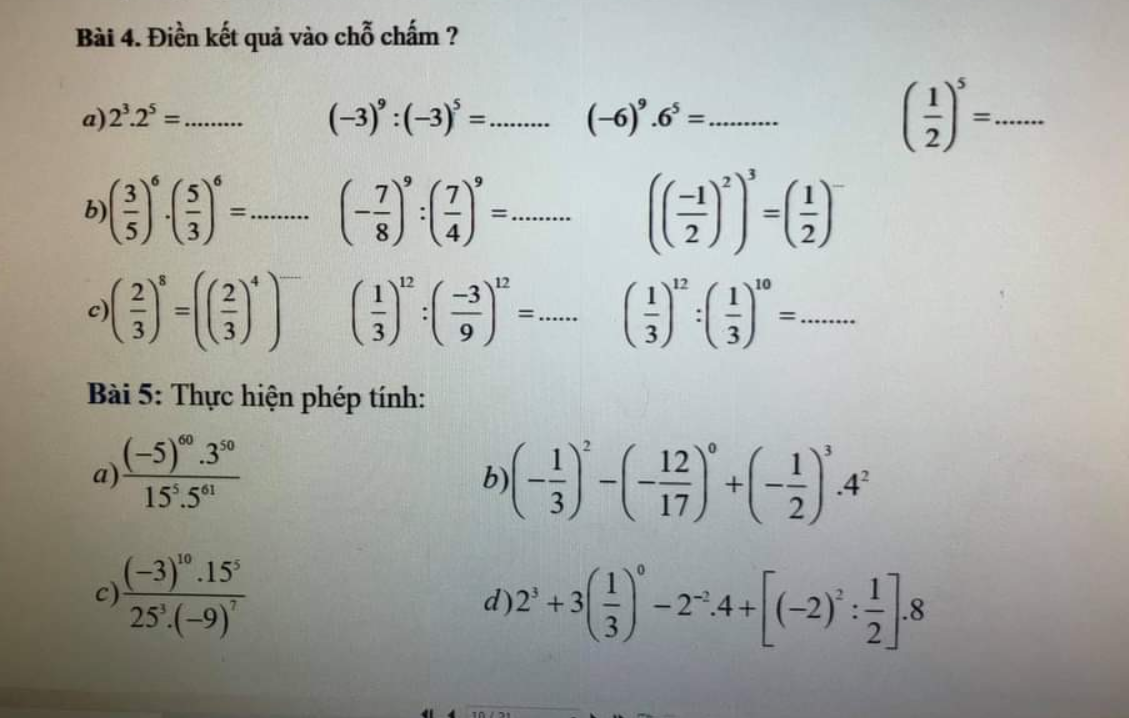
Bài 2 :
a) \(\left(x-3\right)\left(x+7\right)< 0\)
\(\Leftrightarrow\hept{\begin{cases}x-3>0\\x+7< 0\end{cases}}\)hoặc \(\hept{\begin{cases}x-3< 0\\x+7>0\end{cases}}\)
mà \(x+3< x+7\forall x\)
nên \(\hept{\begin{cases}x-3< 0\\x+7>0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x< 3\\x>-7\end{cases}}\)
\(\Leftrightarrow-7< x< 3\)
b) \(\left(2x+1\right)\left(x+5\right)>0\)
\(\Leftrightarrow\hept{\begin{cases}2x+1>0\\x+5>0\end{cases}}\)hoặc \(\hept{\begin{cases}2x+1< 0\\x+5< 0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>-\frac{1}{2}\\x>-5\end{cases}}\)hoặc \(\hept{\begin{cases}x< -\frac{1}{2}\\x< -5\end{cases}}\)
hay \(\orbr{\begin{cases}x>-\frac{1}{2}\\x< -5\end{cases}}\)
Bài 3:
\(A=\frac{\frac{3}{7}-\frac{3}{5}+\frac{3}{11}}{-\frac{2}{7}+\frac{2}{5}-\frac{2}{11}}.\frac{\frac{1}{3}-0,25+0,2}{1\frac{1}{6}-0,875+0,7}+\frac{6}{7}\)
\(=\frac{3\left(\frac{1}{7}-\frac{1}{5}+\frac{1}{11}\right)}{-2\left(\frac{1}{7}-\frac{1}{5}+\frac{1}{11}\right)}.\frac{\frac{1}{3}-\frac{1}{4}+\frac{1}{5}}{\frac{7}{6}-\frac{7}{8}+\frac{7}{10}}+\frac{6}{7}\)
\(=\frac{-3}{2}.\frac{2\left(\frac{1}{6}-\frac{1}{8}+\frac{1}{10}\right)}{7\left(\frac{1}{6}-\frac{1}{8}+\frac{1}{10}\right)}+\frac{6}{7}\)
\(=-\frac{3}{2}.\frac{2}{7}+\frac{6}{7}\)
\(=-\frac{3}{7}+\frac{6}{7}=\frac{3}{7}\)
\(B=\left(-19,75\right)+\left(-45,95\right)+\left(4,75+5,95\right)\)
\(=\left(-19,75+4,75\right)+\left(-45,95+5,95\right)\)
\(=\left(-15\right)+\left(-40\right)=-55\)