PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 12 2021
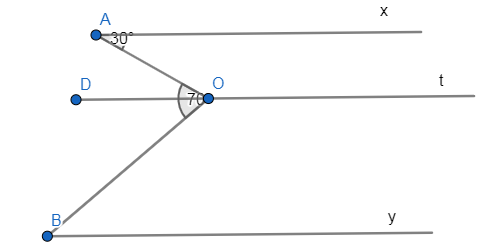
a, Kẻ Ot sao cho Ot song song với Ax và By, ta có:
\(\widehat{xAO}=\widehat{AOD}\) (So le trong)
\(\Rightarrow\widehat{xAO}=\widehat{AOD}=30^0\\\Rightarrow\widehat{DOB}=70^0-30^0=40^0\)
Mà OD//By
\(\Rightarrow\widehat{B}=\widehat{DOB}=40^0\)
AH
Akai Haruma
Giáo viên
21 tháng 8 2023
Lời giải:
Ta thấy:
$\widehat{yBA}+\widehat{BAx}=124^0+56^0=180^0$. Mà 2 góc này ở vị trí trong cùng phía nên $By\parallel Ax$ (đpcm)
KV
30 tháng 8 2023
a) Vẽ tia By' là tia đối của tia By
Ta có:
∠ABy' + ∠ABy = 180⁰ (kề bù)
⇒ ∠ABy' = 180⁰ - ∠ABy
= 180⁰ - 135⁰
= 45⁰
⇒ ∠ABy' = ∠BAx = 45⁰
Mà ∠ABy' và ∠BAx là hai góc so le trong
⇒ By // Ax
b) Ta có:
∠CBy' = ∠ABC - ∠ABy'
= 75⁰ - 45⁰
= 30⁰
⇒ ∠CBy' = ∠BCz = 30⁰
Mà ∠CBy' và ∠BCz là hai góc so le trong
⇒ By // Cz
HN
23 tháng 12 2017
Bài 1:
a) Đồ thị của hàm số y = \(\dfrac{2}{3}\)x là đường thẳng OA với A(3 ; 2)
b) \(2x+\dfrac{3}{4}=\dfrac{-1}{2}\)
\(2x=\dfrac{-1}{2}-\dfrac{3}{4}\)
\(2x=-\dfrac{5}{4}\)
\(x=-\dfrac{5}{4} :2\)
\(x=-\dfrac{5}{8}\)
c) Ta có: x.2 = y.4 \(\Rightarrow\dfrac{x}{4}=\dfrac{y}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\dfrac{x}{4}=\dfrac{y}{2}=\dfrac{x-y}{4-2}=\dfrac{12}{2}=6\)
\(\Rightarrow\left\{{}\begin{matrix}x=6.4=24\\y=6.2=12\end{matrix}\right.\)
Vậy x = 24; y = 12.
HN
23 tháng 12 2017
Bài 2:
a) NB?
Vì M là trung điểm của AB
nên MA = MB = \(\dfrac{AB}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Ta có: \(\left\{{}\begin{matrix}Ax\perp AB\\By\perp AB\end{matrix}\right.\)
\(\Rightarrow Ax//By\)
b) Xét hai tam giác vuông AMP và BMQ có:
MA = MB (gt)
\(\widehat{AMP}=\widehat{BMQ}\) (đối đỉnh)
\(\Rightarrow\Delta AMP=\Delta BMQ\left(cgv-gn\right)\)
\(\Rightarrow\) MP = MQ
Xét hai tam giác AMQ và BMP có:
MA = MB (gt)
\(\widehat{AMQ}=\widehat{BMP}\) (đối đỉnh)
MQ = MP (cmt)
\(\Rightarrow\Delta AMQ=\Delta BMP\left(c-g-c\right)\)
\(\Rightarrow\widehat{AQM}=\widehat{BPM}\)
Mà hai góc này ở vị trí so le trong
\(\Rightarrow\) AQ // BP (đpcm).
23 tháng 12 2017
1)
a)
_ Xác định điểm A(3;2)
_ Đường thẳng OA là đồ thị của hàm số \(y=\dfrac{2}{3}x\)
24 tháng 12 2017
a)Hàm số y=\(\dfrac{2}{3}\)x
Đi qua x=0 \(\rightarrow\)y=0 0(0:0)
x=3\(\rightarrow\)y=2 A(3:2)
21 tháng 5 2018
Có \(x=by+cz\)
=> \(x\left(1+a\right)=ax+x=ax+by+cz\)
=> \(\frac{1}{1+a}=\frac{x}{ax+by+cz}\)
=> \(\frac{a}{1+a}=\frac{ax}{ax+by+cz}\)
Có \(y=cz+ax\)
=> \(y\left(1+b\right)=by+y=by+cz+ax=ax+by+cz\)
=> \(\frac{1}{1+b}=\frac{y}{ax+by+cz}\)
=> \(\frac{b}{1+b}=\frac{by}{ax+by+cz}\)
Có \(z=ax+by\)
=> \(z\left(1+c\right)=cz+z=cz+ax+by=ax+by+cz\)
=> \(\frac{1}{1+c}=\frac{z}{ax+by+cz}\)
=> \(\frac{c}{1+c}=\frac{cz}{ax+by+cz}\)
=> \(M=\frac{a}{1+a}+\frac{b}{1+b}+\frac{c}{1+c}=\frac{ax}{ax+by+cz}+\frac{by}{ax+by+cz}+\frac{cz}{ax+by+cz}\)
\(=\frac{ax+by+cz}{ax+by+cz}=1\)
Vậy giá trị của M là 1
Ta vẽ một đường thẳng Qt đi quaQt//Ax
Ta có: Qt//Ax
Ax//By
=> Qt//By
Vì Qt//Ax nên góc xAQ=AQt= m (so le trong)
Ta lại có: góc AQt+ góc tQB= m+n
m+ góc tQB= m+n
góc tQB= m+n-m
góc TQB= n
Vì Qt// by nên tQB=QBy=n (so le trong)
Vậy QBy= n độ