K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 5 2016
\(y'=\frac{1-\ln x-\left(1-\ln x-1\right)}{x^2\left(1-\ln x\right)^2}=\frac{1}{x^2\left(1-\ln x\right)^2}\)
LT
31 tháng 3 2017
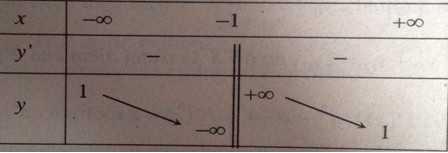
a) y=x+3x+1y=x+3x+1 có tập xác định : R\{-1}
y′=−2(x+1)2<0,∀x≠−1y′=−2(x+1)2<0,∀x≠−1
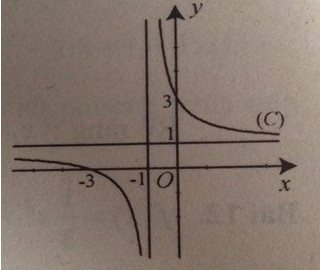
Tiệm cận đứng: x = -1
Tiệm cận ngang: y = 1
Bảng biến thiên:
Đồ thị hàm số:
b) Xét phương trình có nghiệm là hoành độ giao điểm của (C) và đường thẳng (d): y = 2x + m
(1)
x+3x+1=2x+m⇔x+3=(2x+m)(x+1)⇔2x2+(m+1)x+m−3=0,x≠−1x+3x+1=2x+m⇔x+3=(2x+m)(x+1)⇔2x2+(m+1)x+m−3=0,x≠−1
Δ = (m+1)2 – 4.2(m-3) = m2 – 6m + 25 = (m-3)2 + 16> 0, Δm, nên (1) luôn có hai nghiệm phân biệt khác -1.
Vậy (d) luôn cắt (C) tại hai điểm phân biệt M, N (hoành độ của M, N chính là nghiệm của (1)).
BT
29 tháng 5 2017
TenAnh1
C = (-4.24, -6.16)
C = (-4.24, -6.16)
C = (-4.24, -6.16)
D = (11.12, -6.16)
D = (11.12, -6.16)
D = (11.12, -6.16)
E = (-4.28, -6.08)
E = (-4.28, -6.08)
E = (-4.28, -6.08)
F = (11.08, -6.08)
F = (11.08, -6.08)
F = (11.08, -6.08)
Vậy \(Min_{MN}=2\sqrt{3}\) khi \(m=3\).
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 2 2020
\(I=\int\limits^e_1\frac{\frac{1-lnx}{x^2}}{\left(1+\frac{lnx}{x}\right)^2}dx\)
Đặt \(\frac{lnx}{x}=t\Rightarrow\left(\frac{1-lnx}{x^2}\right)dx=dt\)
\(\Rightarrow I=\int\limits^{\frac{1}{e}}_0\frac{dt}{\left(1+t\right)^2}=-\frac{1}{1+t}|^{\frac{1}{e}}_0=\frac{1}{e+1}\)
\(\Rightarrow a=b=1\Rightarrow a^2+b^2=2\)
AH
Akai Haruma
Giáo viên
8 tháng 2 2017
Câu 2)
Đặt \(\left\{\begin{matrix} u=\ln ^2x\\ dv=x^2dx\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=2\frac{\ln x}{x}dx\\ v=\frac{x^3}{3}\end{matrix}\right.\Rightarrow I=\frac{x^3}{3}\ln ^2x-\frac{2}{3}\int x^2\ln xdx\)
Đặt \(\left\{\begin{matrix} k=\ln x\\ dt=x^2dx\end{matrix}\right.\Rightarrow \left\{\begin{matrix} dk=\frac{dx}{x}\\ t=\frac{x^3}{3}\end{matrix}\right.\Rightarrow \int x^2\ln xdx=\frac{x^3\ln x}{3}-\int \frac{x^2}{3}dx=\frac{x^3\ln x}{3}-\frac{x^3}{9}+c\)
Do đó \(I=\frac{x^3\ln^2x}{3}-\frac{2}{9}x^3\ln x+\frac{2}{27}x^3+c\)
AH
Akai Haruma
Giáo viên
8 tháng 2 2017
Câu 3:
\(I=\int\frac{2}{\cos 2x-7}dx=-\int\frac{2}{2\sin^2x+6}dx=-\int\frac{dx}{\sin^2x+3}\)
Đặt \(t=\tan\frac{x}{2}\Rightarrow \left\{\begin{matrix} \sin x=\frac{2t}{t^2+1}\\ dx=\frac{2dt}{t^2+1}\end{matrix}\right.\)
\(\Rightarrow I=-\int \frac{2dt}{(t^2+1)\left ( \frac{4t^2}{(t^2+1)^2}+3 \right )}=-\int\frac{2(t^2+1)dt}{3t^4+10t^2+3}=-\int \frac{2d\left ( t-\frac{1}{t} \right )}{3\left ( t-\frac{1}{t} \right )^2+16}=\int\frac{2dk}{3k^2+16}\)
Đặt \(k=\frac{4}{\sqrt{3}}\tan v\). Đến đây dễ dàng suy ra \(I=\frac{-1}{2\sqrt{3}}v+c\)
AH
Akai Haruma
Giáo viên
30 tháng 11 2018
Lời giải:
Ta có:
\(m\ln (1-x)-\ln x=m\)
\(\Rightarrow m=\frac{\ln x}{\ln (1-x)-1}\)
Đặt \(f(x)=\frac{\ln x}{\ln (1-x)-1}\) \(\Rightarrow f'(x)=\frac{\frac{1}{x}(\ln (1-x)-1)+\frac{1}{1-x}.\ln x}{(\ln (1-x)-1)^2}\)
Với mọi \(x\in (0;1)\) thì \(\ln x< 0; \ln (1-x)< 0\).
\(\Rightarrow \frac{1}{x}(\ln (1-x)-1)+\frac{1}{1-x}.\ln x< 0\)
\(\Rightarrow f'(x)< 0, \forall x\in (0;1)\) hay hàm $f(x)$ nghịch biến trên $(0;1)$
-----------------
Lại có:
\(\lim _{x\to 0+}\frac{\ln x}{\ln (1-x)-1}=\lim_{x\to 0+}\frac{1}{\ln (1-x)-1}.\lim_{x\to +\infty}\ln x\)
\(-1.(-\infty)=+\infty\)
\(\lim_{x\to 1-}\frac{\ln x}{\ln (1-x)-1}=\lim _{x\to 1-}\ln x.\lim_{x\to 1-}\frac{1}{\ln (1-x)-1}=0.0=0\)
Do đó PT có nghiệm khi \(m\in (0;+\infty)\)
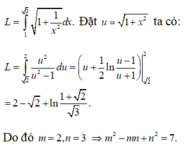
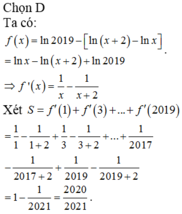
Đề bài là gì vậy bạn?