
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A. Theo quy luật : cứ sau vòng lặp 2 số (vd 7-8) thì số thứ nhất giảm đi 1 đơn vị (vd 7->6) và số thứ 2 tăng lên 1 đơn vị (vd 8->9)

a: =>x+3>0
hay x>-3
b: \(\Leftrightarrow-\left(x-2\right)^2\left(x+2\right)>0\)
=>x+2<0
hay x<-2
c: =>x+4>0
hay x>-4
d: =>-3<x<4

\(\lim\limits_{x\rightarrow1}\frac{x^4+x^3-2}{x^5-x^2}=\lim\limits_{x\rightarrow1}\frac{x^4-1+x^3-1}{x^2\left(x^3-1\right)}\)
\(=\lim\limits_{x\rightarrow1}\frac{\left(x^2-1\right)\left(x^2+1\right)+\left(x-1\right)\left(x^2+x+1\right)}{x^2\left(x-1\right)\left(x^2+x+1\right)}\)\(=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left[\left(x+1\right)\left(x^2+1\right)+\left(x^2+x+1\right)\right]}{x^2\left(x-1\right)\left(x^2+x+1\right)}\)\(=\lim\limits_{x\rightarrow1}\frac{\left[\left(x+1\right)\left(x^2+1\right)+\left(x^2+x+1\right)\right]}{x^2\left(x^2+x+1\right)}\)=\(\frac{7}{3}\)
=lim x^2(x^2+x) - 2 \ x^2(x^3-1)=lim(x^2+x)\(x^3-1)=lim 2\-2=-1

a,\(\dfrac{3x+5}{x-2}=3+\dfrac{11}{x-2}\)
\((3x+5)\vdots (x-2)\) \(\Rightarrow\)\(\dfrac{3x+5}{x-2}\)nguyên \(\Rightarrow \dfrac{11}{x-2}\)nguyên
\(\Rightarrow 11\vdots(x-2)\Rightarrow (x-2)\in Ư(11)=\{\pm1;\pm11\}\)
\(\Rightarrow x\in\{-9;1;3;13\}\)
b,\(\dfrac{2-4x}{x-1}=-4-\dfrac{2}{x-1}\)
\((2-4x)\vdots(x-1)\Rightarrow \dfrac{2-4x}{x-1}\)nguyên\(\Rightarrow \dfrac{2}{x-1}\)nguyên
\(\Rightarrow 2\vdots(x-1)\Rightarrow (x-1)\inƯ(2)=\{\pm1;\pm2\}\\\Rightarrow x\in\{-1;0;2;3\}\)
c,\(\dfrac{x^{2}-x+2}{x-1}=\dfrac{x(x-1)+2}{x-1}=x+\dfrac{2}{x-1}\)
\((x^{2}-x+2)\vdots(x-1)\)\(\Rightarrow \dfrac{x^{2}-x+2}{x-1}\)nguyên \(x+\dfrac{2}{x-1}\)nguyên\(\Rightarrow \dfrac{2}{x-1}\)nguyên
\(\Rightarrow 2\vdots(x-1)\Rightarrow (x-1)\inƯ(2)=\{\pm1;\pm2\}\\\Rightarrow x\in\{-1;0;2;3\}\)
d,\(\dfrac{x^{2}+2x+4}{x+1}=\dfrac{(x+1)^{2}+3}{x+1}=x+1+\dfrac{3}{x+1}\)
\((x^{2}+2x+4)\vdots(x+1)\Rightarrow \dfrac{x^{2}+2x+4}{x+1}\in Z\Rightarrow \dfrac{3}{x+1}\in Z\\\Rightarrow3\vdots(x+1)\Rightarrow (x+1)\in Ư(3)=\{\pm1;\pm3\}\\\Rightarrow x\in\{-4;-2;0;2\}\)

3(x-2)-4(2x+1)-5(2x+3)=50
<=>(3x-6)-(8x+4)-(10x+15)=50
<=>3x-6-8x-4-10x-15=50
<=>(3x-8x-10x)+(-6-4-15)=50
<=>-15x-25=50
<=>-15x=75
<=>x=-5
\(3\frac{1}{2}:\left(4-\frac{1}{3}\left|2x+1\right|\right)=\frac{21}{22}\)
<=>\(4-\frac{1}{3}\left|2x+1\right|=\frac{7}{2}:\frac{21}{22}=\frac{11}{3}\)
<=>\(\frac{1}{3}\left|2x+1\right|=4-\frac{11}{3}=\frac{1}{3}\)
<=>\(\left|2x+1\right|=1\)
<=>2x+1=1 hoặc 2x+1=-1
<=>2x=0 hoặc 2x=-2
<=>x=0 hoặc x=-2
Vậy......................
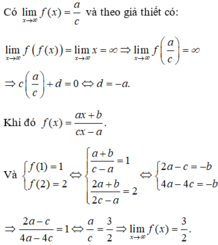
Đáp án B
Ta có: lim x → 5 x 2 − 2 x − 15 2 x − 10 = lim x → 5 x − 5 x + 3 2 x − 5 = lim x → 5 x + 3 2 = 4