
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi 2 số đó là a và b
Ta có: \(\left\{{}\begin{matrix}a+b=\sqrt{19}\\a-b=\sqrt{7}\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}a^2+2ab+b^2=19\\a^2-2ab+b^2=7\end{matrix}\right.\)
<=> \(\left(a^2+2ab+b^2\right)-\left(a^2-2ab+b^2\right)=19-7\)
<=> 4ab = 12
<=> ab = 3



ĐKXĐ: x<>1 và y<>0
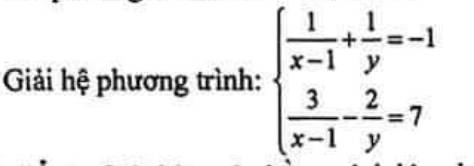
\(\left\{{}\begin{matrix}\dfrac{1}{x-1}+\dfrac{1}{y}=-1\\\dfrac{3}{x-1}-\dfrac{2}{y}=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2}{x-1}+\dfrac{2}{y}=-2\\\dfrac{3}{x-1}-\dfrac{2}{y}=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{x-1}=5\\\dfrac{1}{x-1}+\dfrac{1}{y}=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-1=1\\\dfrac{1}{y}=-1-1=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-\dfrac{1}{2}\end{matrix}\right.\left(nhận\right)\)

https://diendantoanhoc.net/topic/74052-cho-xyz0-xyz1-tim-gtnn-c%E1%BB%A7a-p-fracx2yzyzfracy2zxzxfracz2xyxy/
vào là có ok


a/ Ta có
IH vuông góc AB => ^AHI = 90
IK vuông góc AD => ^AKI = 90
=> H và K cùng nhìn AI dưới hai góc bằng nhau => AHIK là tứ giác nội tiếp
b/ Xét tam giác ADI và tam giác BCI có
^AID=^BIC (góc đối đỉnh)
sđ ^DAC = sđ ^DBC = 1/2 sđ cung CD (góc nội tiếp) => ^DAC=^DBC
=> tg ADI đồng dạng tg BCI
=> \(\frac{IA}{IB}=\frac{ID}{IC}\Rightarrow IA.IC=IB.ID\)
c/
Xét tứ giác nội tiếp AHIK có
^HIK = 180 - ^DAB (hai góc đối của tứ giác nội tiếp bù nhau) (1)
^DAC = ^KHI (2 góc nội tiếp chắn cùng 1 cung) (2)
Xét tứ giác nội tiếp ABCD có
^BCD = 180 - ^DAB (hai góc đối của tứ giác nội tiếp bù nhau) (3)
^DAC = ^DBC (hai góc nội tiếp chắn cùng 1 cung) (4)
Xét hai tam giác HIK và tam giác BCD
Từ (1) và (3) => ^HIK = ^BCD
Từ (2) và (4) => ^KHI = ^DBC
=> tam giác HIK đồng dạng với tam giác BCD

Đk: \(2\le x\le4\)
Áp dụng BĐT bunhiacopxki có:
\(P^2=\left(\sqrt{x-2}+3\sqrt{4-x}\right)^2\le\left(1+3^2\right)\left(x-2+4-x\right)\)
\(\Leftrightarrow P^2\le20\)\(\Leftrightarrow P\le2\sqrt{5}\)
Dấu "=" xảy ra khi \(\sqrt{x-2}=\dfrac{\sqrt{4-x}}{3}\) \(\Leftrightarrow x=\dfrac{11}{5}\) (tm đk)
Có \(P^2=8\left(4-x\right)+6\sqrt{\left(x-2\right)\left(4-x\right)}+2\ge2\)\(\Rightarrow P\ge\sqrt{2}\)
Dấu "=" xảy ra khi x=4 (tm)

 cíu lẹ cíu lẹ
cíu lẹ cíu lẹ 

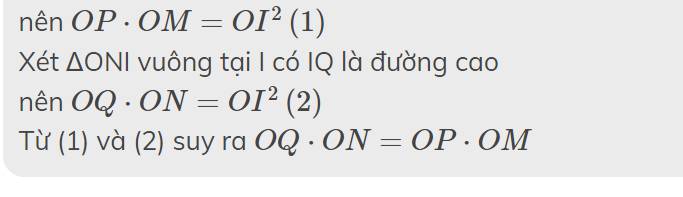
 cíu lẹ ạ!
cíu lẹ ạ!