Làm tính nhân phân thức: x -...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PT

Pham Trong Bach

1 tháng 11 2017

Làm tính nhân phân thức: x - 13 2 2 x 5 . - 3 x 2 x - 13

#Hỏi cộng đồng OLM #Toán lớp 8

1

CM

Cao Minh Tâm

1 tháng 11 2017

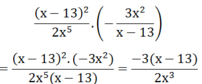
Để học tốt Toán 8 | Giải toán lớp 8

Các câu hỏi dưới đây có thể giống với câu hỏi trên

DT

Đỗ Trung

7 tháng 11 2016

1a) làm tính nhân: -7x(3x-2)b) tính nhanh: 872+26.87+132C2a) phân tích đa thức sau thành nhân tử: x2-25b) tìm x biết: 3x(x+5)-2x-10=0C3Cho 2 đa thức A=3x3-2x2+2 và B=x+1a) thực hiện phép chia A và Bb) tìm số nguyên x để đa thức A chia hết cho đa thức Bgiải hộ mik nhé mik đang cần gấp mai phải nộp rồi các bạn giúp mik nhanh...

#Hỏi cộng đồng OLM #Toán lớp 8

2

KV

Kha Võ Nguyễn Minh

7 tháng 11 2016

a) 3x3-2x2+2 chia x+1= 3x2-5x+5 dư -3 b) -3 chia hết x+1 vậy chon x =2

NN

Nguyễn Nam

10 tháng 11 2017

1)

a) \(-7x\left(3x-2\right)\)

\(=-21x^2+14x\)

b) \(87^2+26.87+13^2\)

\(=87^2+2.87.13+13^2\)

\(=\left(87+13\right)^2\)

\(=100^2\)

\(=10000\)

2)

a) \(x^2-25\)

\(=x^2-5^2\)

\(=\left(x-5\right)\left(x+5\right)\)

b) \(3x\left(x+5\right)-2x-10=0\)

\(\Leftrightarrow3x\left(x+5\right)-\left(2x-10\right)=0\)

\(\Leftrightarrow3x\left(x+5\right)-2\left(x-5\right)=0\)

\(\Leftrightarrow\left(x+5\right)\left(3x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+5=0\\3x-2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\3x=2\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=\dfrac{2}{3}\end{matrix}\right.\)

Vậy..........

3)

a) \(A:B=\left(3x^3-2x^2+2\right):\left(x+1\right)\)

Đại số lớp 8

Vậy \(\left(3x^3-2x^2+2\right):\left(x+1\right)=\left(3x^2-5x-5\right)+7\)

b)

Để \(A⋮B\Rightarrow7⋮\left(x+1\right)\)

\(\Rightarrow\left(x+1\right)\in U\left(7\right)=\left\{-1;1-7;7\right\}\)

Đại số lớp 8

Vì x là số nguyên nên x=0 ; x=6 thì \(A⋮B\)

EN

Emily Nain

22 tháng 12 2020 - olm

Phân tích đa thức thành nhân tử:

\(x^2+x-30\)

Tìm x:

a)\(\left(x-2\right)^2-x\left(x-5\right)=13\)

b)\(4x^3-100x=0\)

#Hỏi cộng đồng OLM #Toán lớp 8

1

NH

Nguyễn Huy Tú

22 tháng 12 2020

Bai 1

\(x^2+x-30=x^2+6x-5x-30=\left(x-5\right)\left(x+6\right)\)

Bai 2

a, \(\left(x-2\right)^2-x\left(x-5\right)=13\)

\(\Leftrightarrow x^2-4x+4-x^2+5x=13\)

\(\Leftrightarrow x+4=13\Leftrightarrow x=9\)

b, \(4x^3-100x=0\Leftrightarrow x\left(4x^2-100\right)=0\)

\(\Leftrightarrow x\left(2x-10\right)\left(2x+10\right)=0\Leftrightarrow x=0;\pm5\)

PT

Phạm Thị Huyền Trang

22 tháng 6 2017 - olm

Phân tích đa thức thành nhân tử\(x^3+y^3+z^3-3xyz\).

2)\(25x^2-12x-13\).

3)\(2y^2-3y-5\)

#Hỏi cộng đồng OLM #Toán lớp 8

4

TH

Thanh Hà

22 tháng 6 2017

\(2,25x^2-12x-13\)

\(=25x^2-25x+13x-13\)

\(=25x\left(x-1\right)+13\left(x-1\right)\)

\(=\left(x-1\right)\left(25x+13\right)\)

\(3,2y^2-3y-5\)

\(=2y^2+2y-5y-5\)

\(=2y\left(y+1\right)-5\left(y+1\right)\)

\(=\left(y+1\right)\left(2y-5\right)\)

Còn bài 1 mik đang nghĩ, khi nào biết mik trả lời nha!!!

Chúc bn học giỏi!!!

PT

Phạm Thị Huyền Trang

22 tháng 6 2017

giúp Mk Mk tk

TT

Tran Thi Ha Phuong

12 tháng 8 2018 - olm

phân tích đa thức thành nhân tử:a) \(x^4+2x^3+5x^2+4x-12\)

b)\(x^3-2x^2+2x-13\)

#Hỏi cộng đồng OLM #Toán lớp 8

1

KT

Không Tên

12 tháng 8 2018

a) \(x^4+2x^3+5x^2+4x-12\)

\(=x^4+x^3+6x^2+x^3+x^2+6x-2x^2-2x-12\)

\(=x^2\left(x^2+x+6\right)+x\left(x^2+x+6\right)-2\left(x^2+x+6\right)\)

\(=\left(x^2+x+6\right)\left(x^2+x-2\right)\)

\(=\left(x^2+x+6\right)\left(x-1\right)\left(x+2\right)\)

NM

Nguyễn Minh Đăng

22 tháng 7 2020 - olm

Phân tích đa thức thành nhân tử:

\(f\left(x\right)=x^4+8x^3+28x^2+48x-13\)

#Hỏi cộng đồng OLM #Toán lớp 8

2

TL

Tran Le Khanh Linh

22 tháng 7 2020

\(f\left(x\right)=x^4+8x^3+28x^2+48x-13\)

\(=\left(x^4+4x^3+7x^2\right)+\left(4x^3+16x^2+28x\right)+\left(5x^2+20x+35\right)-48\)

\(=x^2\left(x^2+4x+7\right)+4x\left(x^2+4x+7\right)+5\left(x^2+4x+7\right)-48\)

\(=\left(x^2+4x+7\right)\left(x^2+4x+5\right)-48\)

đặt t=\(x^2+4x+6\)khi đó g(t)=(t-1)(t+1)-48=t²-49=(t-7)(y+7)

vậy f(x)=(x²+4x-1)(x²+4x+13)

KA

Kiyotaka Ayanokoji

22 tháng 7 2020

Trả lời:

Thay \(f\left(x\right)=0\), ta có:

\(0=x^4+8x^3+28x^2+48x-13\)

\(\Leftrightarrow-x^4-8x^3-28x^2-48x+13=0\)

\(\Leftrightarrow-x^4-4x^3-4x^3+x^2-16x^2-13x^2+4x-56x+13=0\)

\(\Leftrightarrow\left(-x^4-4x^3+x^2\right)+\left(-4x^3-16x^2+4x\right)+\left(-13x^2-56x+13\right)=0\)

\(\Leftrightarrow-x^2.\left(x^2+4x-1\right)-4x.\left(x^2+4x-1\right)-13.\left(x^2+4x-1\right)=0\)

\(\Leftrightarrow\left(-x^2-4x-13\right).\left(x^2+4x-1\right)=0\)

Vì \(-x^2-4x-13=-x^2-4x-4-9\)

\(=-\left(x^2+4x+4\right)-9\)

\(=-\left(x+2\right)^2-9< 0\forall x\)

\(\Rightarrow x^2+4x-1=0\)

\(\Leftrightarrow\left(x^2+4x+4\right)-5=0\)

\(\Leftrightarrow\left(x+2\right)^2=5=\left(\pm\sqrt{5}\right)^2\)

\(\Leftrightarrow\orbr{\begin{cases}x+2=\sqrt{5}\\x+2=-\sqrt{5}\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=-2+\sqrt{5}\\x=-2-\sqrt{5}\end{cases}}\)

Vậy đa thức có 2 nghiêm \(x\in\left\{-2+\sqrt{5},-2-\sqrt{5}\right\}\)

SG

Sách Giáo Khoa

28 tháng 4 2017

Làm tính cộng các phân thức :

a) \(\dfrac{11x+13}{3x-3}+\dfrac{15x+17}{4-4x}\)

b) \(\dfrac{2x+1}{2x^2-x}+\dfrac{32x^2}{1-4x^2}+\dfrac{1-2x}{2x^2+x}\)

c) \(\dfrac{1}{x^2+x+1}+\dfrac{1}{x^2-x}+\dfrac{2x}{1-x^3}\)

d) \(\dfrac{x^4}{1-x}+x^3+x^2+x+1\)

#Hỏi cộng đồng OLM #Toán lớp 8

1

NT

Nguyen Thuy Hoa

28 tháng 6 2017

Phép cộng các phân thức đại số

PL

Phương Linh

21 tháng 6 2016 - olm

phân tich đa thức thành nhân tử

\(\left(x+1\right)^2-3\left(x+13\right)\)

\(3x\left(x-1\right)^2-\left(1-x\right)^3\)

#Hỏi cộng đồng OLM #Toán lớp 8

1

MA

minh anh

21 tháng 6 2016

\(\left(x+1\right)^2-3\left(x+13\right)=x^2+2x+1-3x-39\)

\(=x ^2-x-38\)

\(=x^2-2.\frac{1}{2}x+\frac{1}{4}-\frac{153}{4}\)

\(=\left(x-\frac{1}{2}\right)^2-\sqrt{\frac{153}{4}}^2\)

\(=\left(x-\frac{1}{2}-\sqrt{\frac{153}{4}}\right)\left(x-\frac{1}{2}+\sqrt{\frac{153}{4}}\right)\)

\(=\left(x-\frac{1+\sqrt{153}}{2}\right)\left(x-\frac{1-\sqrt{153}}{2}\right)\)

K

©ⓢ丶κεη春╰‿╯

24 tháng 2 2020 - olm

B3 : a) Làm Tính Nhân : \(\left(4x^3-xy^2+y^3\right)\left(x^2y+2xy^2-2y^3\right)\)b) Phân tích đa thức thành nhân tử :(!) \(2\left(x+y\right)^2-7\left(x+y\right)+5\)(!!) \(\left(x+y+z\right)^2-x^2-y^2-z^2\)c) Tính GTBT : \(x^3-y^3-x^2-y^2-11xy\) biết \(x-y=3\)d)Tìm giá trị biểu thức của a và b để...

#Hỏi cộng đồng OLM #Toán lớp 8

2

KN

Kiệt Nguyễn

24 tháng 2 2020

a)\(\left(4x^3-xy^2+y^3\right)\left(x^2y+2xy^2-2y^3\right)\)

\(=x^2y\left(4x^3-xy^2+y^3\right)+2xy^2\left(4x^3-xy^2+y^3\right)\)

\(-2y^3\left(4x^3-xy^2+y^3\right)\)

\(=4x^5y-x^3y^3+x^2y^4+8x^4y^2-2x^2y^4+2xy^5\)

\(-8x^3y^3+2xy^5-2y^6\)

\(=-2y^6+4x^5y+\left(2xy^5+2xy^5\right)+8x^4y^2+\left(x^2y^4-2x^2y^4\right)\)

\(-\left(x^3y^3+8x^3y^3\right)\)

\(=-2y^6+4x^5y+4xy^5+8x^4y^2-x^2y^4-9x^3y^3\)

KN

Kiệt Nguyễn

24 tháng 2 2020

b)

(!) \(2\left(x+y\right)^2-7\left(x+y\right)+5\)

\(=2\left(x+y\right)^2-2\left(x+y\right)-5\left(x+y\right)+5\)

\(=2\left(x+y\right)\left(x+y-1\right)-5\left(x+y-1\right)\)

\(=\left(2x+2y-5\right)\left(x+y-1\right)\)

(!!) \(\left(x+y+z\right)^2-x^2-y^2-z^2\)

\(=\left(x^2+y^2+z^2+2xy+2yz+2zx\right)-x^2-y^2-z^2\)

\(=2\left(xy+yz+zx\right)\)

SG

Sách Giáo Khoa

21 tháng 4 2017

Áp dụng quy tắc đổi dấu để các phân thức có cùng mẫu thức rồi làm tính cộng phân thức :

a) \(\dfrac{2x^2-x}{x-1}+\dfrac{x+1}{1-x}+\dfrac{2-x^2}{x-1}\)

b) \(\dfrac{4-x^2}{x-3}+\dfrac{2x-2x^2}{3-x}+\dfrac{5-4x}{x-3}\)

#Hỏi cộng đồng OLM #Toán lớp 8

2

AT

Anh Triêt

21 tháng 4 2017

Giải bài 22 trang 46 Toán 8 Tập 1 | Giải bài tập Toán 8

DT

ĐứcLĩnh TH

30 tháng 11 2021

Giải bài 22 trang 46 Toán 8 Tập 1 | Giải bài tập Toán 8

VL

Võ Lý Anh Thư

27 tháng 9 2018 - olm

1- Tìm x để biểu thức 3−x2+2x3−x2+2x có giá trị lớn nhất .2- Tìm x để biểu thức 3(2x+9)2−13(2x+9)2−1 có giá trị nhỏ nhất3- Tìm giá trị rút gọn của (x−1)(x+2)−(x+1)x(x−1)(x+2)−(x+1)x4- 511<a11<711511<a11<711 . Tìm số a thỏa mãn5- Giá trị nhỏ nhất của M=|x+3|+|x-5|6- Giá trị lớn nhất của A=|x+13|+647- Bậc của đơn thức 12x2y5z312x2y5z38- (13)2017×32016×21(13)2017×32016×219- Nghiệm của đa...

#Hỏi cộng đồng OLM #Toán lớp 8

0