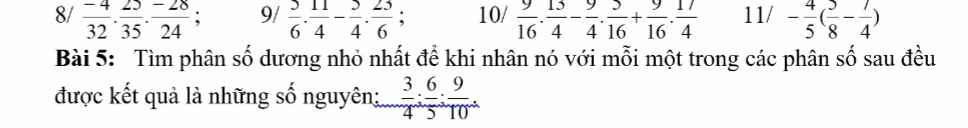Làm hộ mình câu c bài 3 bài 4 5 6

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

TD

Trần Đan Thoả

12 tháng 3 2021 - olm

Làm hộ mình câu c bài 3 bài 4 5 6

1

NT

Nguyễn Thu Hà

12 tháng 3 2021

Nhưng bài đâu mà làm hả bn

Các câu hỏi dưới đây có thể giống với câu hỏi trên

M

Manhmoi

23 tháng 12 2021

mn ơi làm hộ mình câu này với,ai làm nhanh nhất mình tim cho ! bài 5:tìm các số nguyên x,y biết : xy + x + y =...

1

NH

Nguyễn Hoàng Tùng

23 tháng 12 2021

\(xy+x+y=4\\ x\left(y+1\right)+y+1=4+1=5\\ \left(x+1\right)\left(y+1\right)=5\)

\(x+1\)	\(5\)	\(1\)	\(-1\)	\(-5\)
\(y+1\)	\(1\)	\(5\)	\(-5\)	\(-1\)
\(x\)	\(4\)	\(0\)	\(-2\)	\(-6\)
\(y\)	\(0\)	\(4\)	\(-6\)	\(-2\)

TD

Thuỳ Dương

9 tháng 8 2021

Làm hộ câu c bài 4

2

TD

Thuỳ Dương

9 tháng 8 2021

làm hộ luôn câu 4

TD

Thuỳ Dương

9 tháng 8 2021

câu d

VT

Vũ Thị Thanh Hà

14 tháng 6 2020 - olm

Lô anh em, làm hộ mình bài này với ( đang cần rất gấp, mai k có bài cô đánh nát mông)

Tính :

B = 1 . 3 + 2 . 5 + 3 . 6 + ...... + 99 . 102

0

T

TrầnHoàngGiang

30 tháng 10 2023 - olm

Mọi người làm giúp mình bài 2, 3, 5 hộ mình ạ!

1

NN

Nguyễn Ngọc Anh Minh

CTVHS VIP

31 tháng 10 2023

2/

a/

\(\dfrac{4n+2}{n+1}=\dfrac{4n+4-2}{n+1}=\dfrac{4\left(n+1\right)-2}{n+1}=4-\dfrac{2}{n+1}\)

\(\Rightarrow4n+2⋮n+1\) Khi \(n+1=\left\{-2;-1;1;2\right\}\Rightarrow n=\left\{-3;-2;0;1\right\}\)

b/

\(\Rightarrow a+2=\dfrac{8}{b-1}\left(b\ne1\right)\) (1)

a nguyên => a+2 nguyên \(\Rightarrow8⋮\left(b-1\right)\)

\(\Rightarrow b-1=\left\{-8;-4;-2;-1;1;2;4;8\right\}\)

\(\Rightarrow b=\left\{-7;-3;-1;0;2;3;5;9\right\}\) Thay các giá trị của b vào (1) để tìm a

3/

Gọi số tiền mẹ cho Chi là A \(\Rightarrow100000\le A\le200000\)

Nếu bớt số tiền mẹ cho Chi đi 5000 đồng thì

\(A-5000⋮15000;A-5000⋮8000\)

\(\Rightarrow A-5000=UC\left(8000;15000\right)\) Và \(95000\le A-5000\le195000\)

\(\Rightarrow A-5000=120000\Rightarrow A=125000\)

NM

nguyen minh huyen

3 tháng 7 2019 - olm

Tính:

A=1 +2 +2 ^2 +.............+2^100

B=1 +3 ^2 +3^4 +3^6 +...............3^100

C=1 +5^3 +5^6 +.......................+5^99

AI NHANH MÌNH SẼ TICK ĐÚNG LUÔN ,CỐ GẮNG LÀM TRỌN 3 CÂU HỘ MÌNH NHA

Giai hộ mình trong vòng tối từ 7-9 h mình sẽ lấy cả máy của bạn mình tick đ cho nha

3

T

T.Ps

3 tháng 7 2019

#)Giải :

\(A=1+2+2^2+...+2^{100}\)

\(2A=2+2^2+2^3+...+2^{101}\)

\(2A-A=\left(2+2^2+2^3+...+2^{101}\right)-\left(1+2+2^2+...+2^{100}\right)\)

\(A=2^{101}-1\)

\(B=1+3^2+3^4+...+3^{100}\)

\(3^2B=3^2+3^4+3^6+...+3^{102}\)

\(3^2B-B=\left(3^2+3^4+3^6+...+3^{102}\right)-\left(1+3^2+3^4+...+3^{100}\right)\)

\(8B=3^{102}-1\)

\(B=\frac{3^{102}-1}{8}\)

\(C=1+5^3+5^6+...+5^{99}\)

\(5^2C=5^3+5^6+5^9+...+5^{102}\)

\(5^2C-C=\left(5^3+5^6+5^9...+5^{102}\right)-\left(1+5^3+5^6+...+5^{99}\right)\)

\(24C=5^{102}-1\)

\(C=\frac{5^{102}-1}{24}\)

XO

Xyz OLM

3 tháng 7 2019

a) A = 1 + 2² + ... + 2¹⁰⁰

=> 2A = 2² + 2³ + ... + 2¹⁰¹

Lấy 2A - A = (2 + 2² + ... + 2¹⁰¹) - (1 + 2² + ... 2¹⁰⁰)

A = 2¹⁰¹ - 1

b) B = 1 + 3² + 3⁴ + ... + 3¹⁰⁰

=> 3²B = 3² + 3⁴ + 3⁶ + ..... + 3¹⁰²

=> 9B = 3² + 3⁴ + 3⁶ + ..... + 3¹⁰²

Lấy 9B - B = ( 3² + 3⁴ + 3⁶ + ..... + 3¹⁰²) - (1 + 3² + 3⁴ + ... + 3¹⁰⁰)

8B = 3¹⁰² - 1

B = \(\frac{3^{102}-1}{8}\)

c) C = 1 + 5³ + 5⁶ + ... + 5⁹⁹

=> 5³.C = 5³ . 5⁶ . 5⁹ + ... + 5¹⁰²

=> 125.C = 5³ . 5⁶ . 5⁹ + ... + 5¹⁰²

Lấy 125.C - C = (5³ . 5⁶ . 5⁹ + ... + 5¹⁰²) - (1 + 5³ + 5⁶ + ... + 5⁹⁹)

124.C = 5¹⁰² - 1

=> C = \(\frac{5^{102}-1}{124}\)

DN

Đặng Ngọc Bảo Trang

9 tháng 2 2023 - olm

Bài 4:Tính

a. 7/8 + 1/2 b. 5/6 + (-2) c. 2/5 + -3/8 d. 5/7 - 3/8 e. 3/4 - 1/2 +7/6

làm trong hôm nay nha mình cần gấp lắm

2

NT

Nguyễn thành Đạt

9 tháng 2 2023

\(a.\dfrac{7}{8}+\dfrac{1}{2}\text{=}\dfrac{11}{8}\)

\(b.\dfrac{5}{6}+\left(-2\right)\text{=}\dfrac{-7}{6}\)

\(c.\dfrac{2}{5}+\dfrac{-3}{8}\text{=}\dfrac{1}{40}\)

\(d.\dfrac{5}{7}-\dfrac{3}{8}\text{=}\dfrac{19}{56}\)

\(e.\dfrac{3}{4}-\dfrac{1}{2}+\dfrac{7}{6}\text{=}\dfrac{17}{12}\)

H

⭐Hannie⭐

9 tháng 2 2023

`a. 7/8 + 1/2 = 7/8 + 4/8=(7+4)/8=11/8`

`b. 5/6 + (-2) =5/6 + (-12/6)=-7/6`

`c. 2/5 + -3/8 = 16/40 + (-15/40)=1/40`

`d. 5/7 - 3/8 = 40/56 - 21/56=19/56`

`e. 3/4 - 1/2 +7/6= 3/4 - 2/4 + 7/6= 1/4 + 7/6= 6/24 + 28/24= 34/24=17/12`

DP

Đặng Phương Nhung

7 tháng 8 2015 - olm

bài 1: cho A=3 + 3^2 + 3^3 +......+3^60. Chứng minh rằnga)A chia hết 4 b)A chia hết 13bài 2: CMR: (12a + 36b) chia hết 12 với a,b thuộcNbài 3:cho a,b,c thuộc N và (111a + 23b) chia hết 12CMR: (9a + 13b) chia hết cho 12bài 4: CMRa) 5 + 5^2 + 5^3 chia hết cho 5b) 2^9 + 2^10 + 2^11 + 2^12 chia hết cho 15c) 10^11 + 8 chia hét cho 3d) 3^20 + 3^19 - 3^18 chia hết 11bài 5: cho A = 8n + 111....1( n chữ số 1)CMR: A chia hết 9ai làm được đủ hết...

1

NT

Nguyễn Thị Tố Nữ

5 tháng 10 2015

Giải

Bài 1:

a) Ta có: A=3+3²⁺3³⁺3⁴+........+3⁵⁹+3⁶⁰=(3+3²)+(3³+3⁴)+..........+(3⁵⁹⁺3⁶⁰)

=12+3²x (3+3²)+.......+3⁵⁸x (3+3²)=12+3²x 12+..........+3⁵⁸ x 12

=12 x (3² +...............+3⁵⁸)= 4 x 3 x (3² +...............+3⁵⁸)

Vì: m.n=m.n chia hết cho n hoặc m. Mà ở đây ta có 4 chia hết cho4.

=> Tổng này chia hết cho 4.

Bài 2:

Ta có: 12a chia hết cho 12; 36b chia hết cho 12.

=> tổng này chia hết cho 12.

Bài 4:a) Ta có: 5 + 5^2 + 5^3= 5 + (.........5) + (............5) = (............5)

Vậy tổng này có kết quả có chữ số tận cùng là 5. Mà những số có chữ số tận cùng là 5 thì chia hết cho 5.

=> Tổng này chia hết cho 5.

DA

Đỗ Anh Thư

22 tháng 2 2022

Làm hộ mình bài 5

0

DH

Đào Hải Long

13 tháng 10 2023 - olm

(N+6):(n+1) làm hộ mình mai mình phải nộp bài này rồi

3

DD

David Dương

13 tháng 10 2023

n= -1 ; -5 ; 1; 5

MH

Minh Hiếu

13 tháng 10 2023

\(n+6⋮n+1\)

\(\Rightarrow5⋮n+1\)

\(\Rightarrow\left(n+1\right)\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)

\(n\in\left\{-6;-2;0;4\right\}\)

LN

Lê Nhật Linh

11 tháng 9 2016 - olm

Giair hộ mình với. Tomorrow mình đi học rồi. Nha!

Đề bài: 2 . 3 . 4 + 3 . 4 . 5 + 4 . 5 . 6 +...+ 100 - 101 . 102

P/S: Bạn nào biết cố gắng giải nhanh giùm mình nhé!

0