K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TB
2
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 4 2021
(O) và (D) cắt nhau tại A và M \(\Rightarrow AM\perp OD\)
\(\Rightarrow\widehat{AOD}=\widehat{ABN}\) (cùng phụ \(\widehat{BAM}\))
\(\Rightarrow OD||BN\) (góc đồng vị bằng nhau)
\(\Rightarrow OBND\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow OB=DN\), mà \(\left\{{}\begin{matrix}AB=DC\\OB=\dfrac{1}{2}AB\end{matrix}\right.\) \(\Rightarrow OB=\dfrac{1}{2}CD\Rightarrow DN=\dfrac{1}{2}DC\Rightarrow N\) là trung điểm CD
Like cho mình nhé !!
29 tháng 8 2021
thay \(x=3-2\sqrt{2}\) vào P ta có:
\(\dfrac{x+8}{\sqrt{x}+1}=\dfrac{3-2\sqrt{2}+8}{\sqrt{3-2\sqrt{2}}+1}=\dfrac{11-2\sqrt{2}}{\sqrt{2}-1+1}=\dfrac{11-2\sqrt{2}}{\sqrt{2}}\)
29 tháng 8 2021
\(b,x=3-2\sqrt{2}=\left(\sqrt{2}-1\right)^2\)
Thay vào P, ta được:
\(P=\dfrac{3-2\sqrt{2}+8}{\sqrt{\left(\sqrt{2}-1\right)^2}+1}=\dfrac{11-2\sqrt{2}}{\sqrt{2}}=\dfrac{11\sqrt{2}-4}{2}\)
TG
1
9 tháng 12 2021
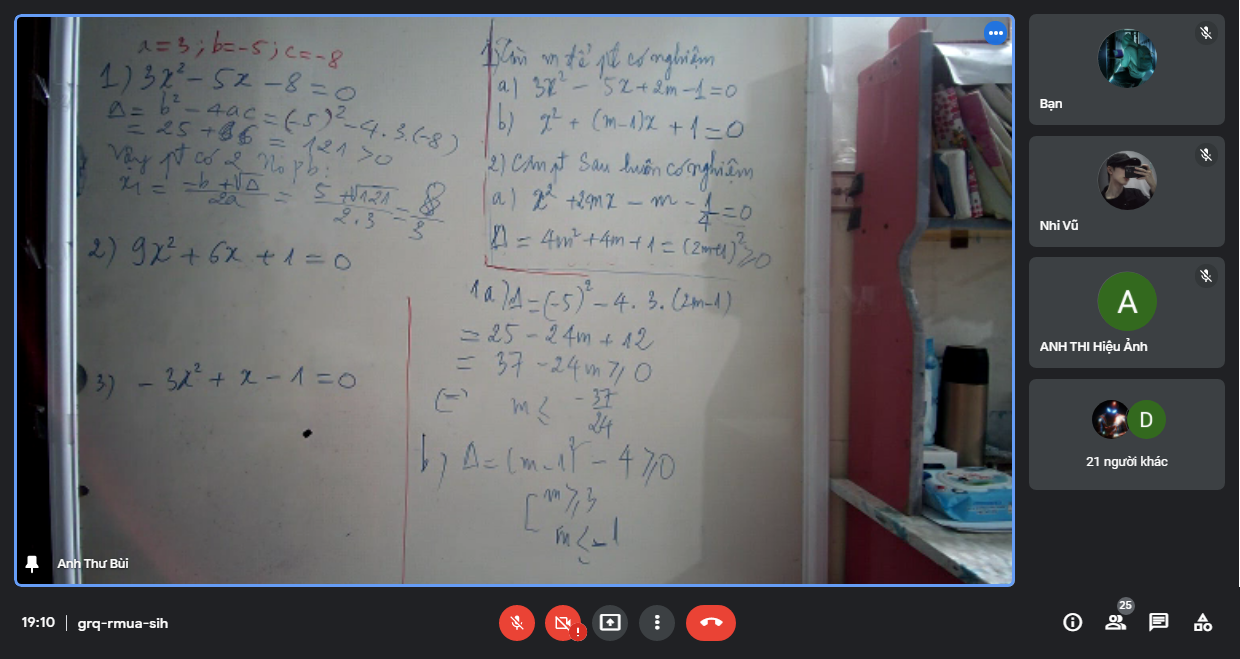
Bài 5:
\(\text{Δ}=\left(3k-2\right)^2+12\left(3k+1\right)\)
\(=9k^2-12k+4+36k+12\)
\(=9k^2+24k+16=\left(3k+4\right)^2>=0\)
Vậy: Phương trình luôn có nghiệm với mọi k
TG
0
5 tháng 9 2021
a: Xét tứ giác AMHK có
\(\widehat{MAK}=\widehat{AKH}=\widehat{AMH}=90^0\)
Do đó: AMHK là hình chữ nhật
Suy ra: AH=KM(1)
Xét ΔAHC vuông tại H có
\(AM\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AC=MK^2\)
NN
2
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
10 tháng 9 2023
Tuỳ vào bài đó như thế nào
Có những bài có độ chính xác cao em nên giữ nguyên kết quả
Nhưng nguyên tắc làm tròn thì 4,9014 thì làm tròn xuống 4,9 thui chứ không làm tròn lên 5 nha
A
1
12 tháng 12 2021
a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp
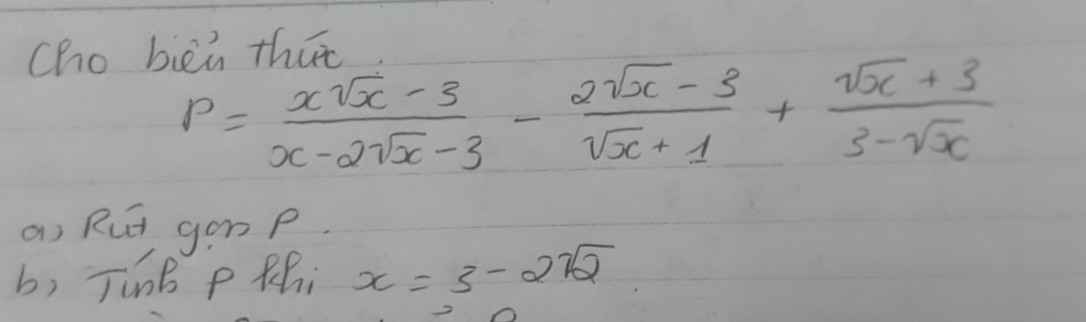
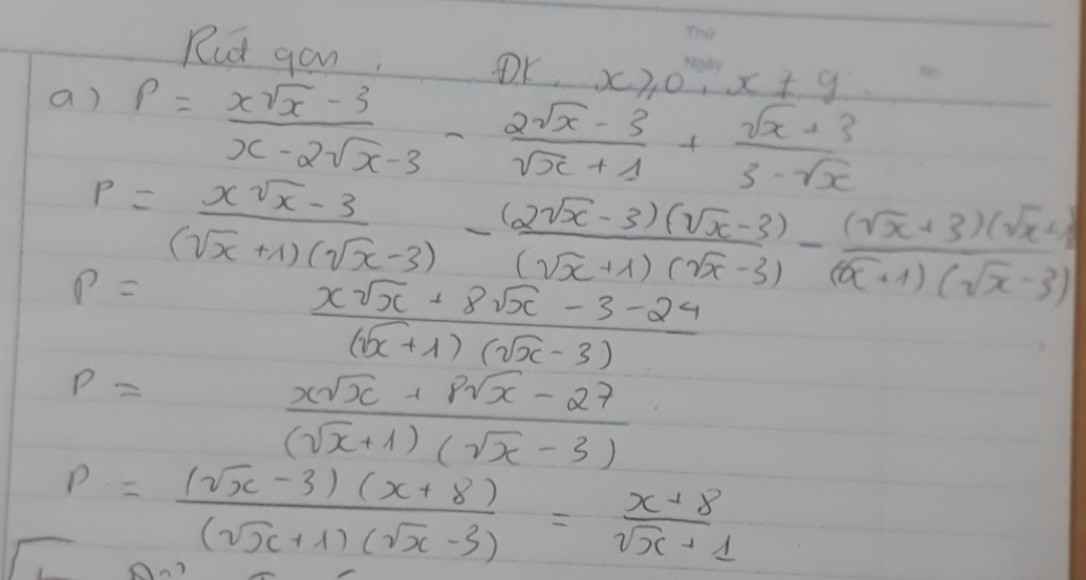
where?