Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,x^2-113=31\\ \Leftrightarrow x^2=144\\ \Leftrightarrow x=\pm12\\ Vay...\\ b,\sqrt{x+2,29}=2.3\\ \Leftrightarrow x+2,29=6^2\\ x=36-2,29=33,71\\ c,x^4=256\\ \Leftrightarrow x=\pm4\\ Vay...\\ d,\left(\sqrt{x}-1\right)^2=0,5625\\ \Leftrightarrow\sqrt{x}-1\in\left\{-0,75;0,75\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{0,25;1,75\right\}\\ Vay...\\ e,2\sqrt{x}-x=0\\ \Leftrightarrow\sqrt{x}\left(2-\sqrt{x}\right)=0\\ \Leftrightarrow\sqrt{x}=0hoac2-\sqrt{x}=0\\ \Leftrightarrow x=0hoacx=4\\ f,x+\sqrt{x}=0\\ \Leftrightarrow\sqrt{x}\left(\sqrt{x}+1\right)=0\\ \Leftrightarrow x=0hoacx=1\)
a. x2−113=31
=> x2=144
=> x2=\(\sqrt{144}\)
=> x=\(\pm12\)
c.x4=256
=> x4=44
=> x=\(\pm4\)


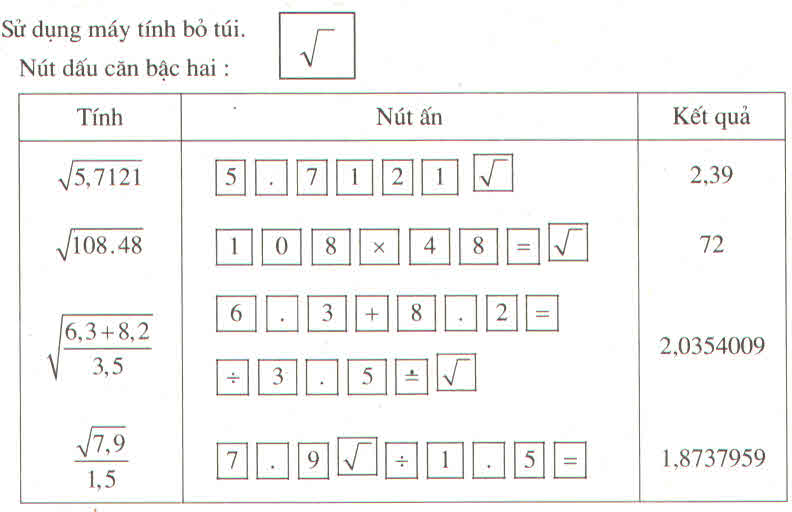
Chú ý: Trong các kết quả trên, hai kết quả đầu là căn bậc hai đúng, hai kết quả cuối là căn bậc hai gần đúng chính xác đến 6 chữ số thập phân (được làm tròn đến chữ số thập phân thứ sáu)

a) \(\dfrac{1}{9}.27^n=3^n\)
\(\dfrac{1}{3^2}.3^{3n}=3^n\\ \Rightarrow3^{3n-2}=3^n\\ \Rightarrow3n-2=n\\ \Rightarrow n=1\)
b) \(3^{-2}.3^4.3^n=3^7\)
\(\dfrac{1}{3^2}.3^4.3^n=3^7\\ \Rightarrow3^{n+2}=3^7\Rightarrow n+2=7\\ \Rightarrow n=5\)
c) \(2^{-1}.2^n+4.2^n=9.2^5\)
\(\dfrac{1}{2}.2^n+4.2^n=9.2^5\\ \Rightarrow2^n\left(\dfrac{1}{2}+4\right)=9.2^5\\ \Rightarrow2^{n-1}.9=9.2^5\\ \Rightarrow n-1=5\\ \Rightarrow n=6\)
d) \(32^{-n}.16^{-n}=2048\)
\(\dfrac{1}{2^n.16^n}.16^n=2^{11}=\dfrac{1}{2^n}=2^{11}\\ \Rightarrow2^n.2^{11}=1\\ \Rightarrow2^{n+11}=2^0\\ \Rightarrow n+11=0\\ \Rightarrow n=-11\)
Chúc bạn học tốt

Bài 5:
a: \(\dfrac{x+7}{x-5}< 0\)
=>x+7>0 và x-5<0
=>-7<x<5
b: \(\dfrac{x-4}{x+9}>0\)
=>x-4>0 hoặc x+9<0
=>x>4 hoặc x<-9
c: \(\dfrac{x-1}{x+9}>1\)
\(\Leftrightarrow\dfrac{x-1-x-9}{x+9}>0\)
=>x+9>0
hay x>-9
d: \(\dfrac{x+5}{x-11}< 1\)
\(\Leftrightarrow\dfrac{x+5-x+11}{x-11}< 0\)
=>x-11<0
hay x<11

1. đề bạn ghi rõ lại giúp mình đc ko r mình giải lại cho
2. Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{2x^2}{2.3^2}=\dfrac{y^2}{5^2}=\dfrac{2x^2-y^2}{18-25}=\dfrac{-28}{-7}=4\)
\(\dfrac{x}{3}=4\Rightarrow x=12\)
\(\dfrac{y}{5}=4\Rightarrow y=20\)
Vậy x=12 và y=20

Lời giải:
Quy nạp:
Xét \(n=1\Rightarrow 2^{3^n}+1=9\) chia hết cho $3$
Xét \(n=2\Rightarrow 2^{3^n}+1=513\) chia hết cho $9$
........
Giả sử điều trên đúng với $n=k$. Ta cần cm nó cũng đúng với $n=k+1$, tức là \(2^{3^{k+1}}+1\vdots 3^{k+1}\)
Thật vậy:
Với giả sử trên, ta có \(2^{3^k}+1\vdots 3^k\)
Có: \(2^{3^{k+1}}+1=(2^{3^k})^3+1=(2^{3^k}+1)(2^{3^k.2}-2^{3^k}+1)\)
Thấy rằng \(2^{3^k}+1\vdots 3^k\)
\(\left\{\begin{matrix} 2^{2.3^k}=4^{3^k}\equiv 1^{3^k}\equiv 1\pmod 3\\ 2^{3^k}\equiv (-1)^{3^k}\equiv -1\pmod 3\\ 1\equiv 1\pmod 3\end{matrix}\right.\Rightarrow 2^{2.3^k}-2^{3^k}+1\equiv 3\equiv 0\pmod 3\)
Hay \(2^{2.3^k}-2^{3^k}+1\vdots 3\)
Suy ra \(2^{3^{k+1}}+1=(2^{3^k}+1)(2^{2.3^k}-2^{3^k}+1)\vdots 3^{k+1}\)
Do đó ta có đpcm.


a,Ta có \(\left(3^3\right)^n:3^n=9\Leftrightarrow3^{3n}:3^n=3^2\Leftrightarrow3n-n=2\Leftrightarrow n=1\)
b,TA có \(\dfrac{5^2}{5^n}=5^1\Leftrightarrow2-n=1\Leftrightarrow n=1\)
Các câu sau để bn tự làm
a) 27n : 3n = 9
\(\Leftrightarrow\) (27 : 3)n = 9
\(\Leftrightarrow\) 9n = 9
\(\Leftrightarrow\) n = 1
b) \(\dfrac{25}{5^n}=5\)
\(\Leftrightarrow\dfrac{5^2}{5^n}=5\)
\(\Leftrightarrow5^n.5=5^2\)
\(\Leftrightarrow5^{n+1}=5^2\)
\(\Leftrightarrow n+1=2\)
n = 2 - 1
n = 1
c) \(\dfrac{81}{\left(-3\right)^n}=-243\)
\(\Leftrightarrow\dfrac{\left(-3\right)^4}{\left(-3\right)^n}=\left(-3\right)^5\)
\(\Leftrightarrow\left(-3\right)^n.\left(-3\right)^5=\left(-3\right)^4\)
\(\Leftrightarrow\left(-3\right)^{n+5}=\left(-3\right)^4\)
\(\Leftrightarrow n+5=4\)
n = 4 - 5
n = -1