K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
2
MN
20 tháng 2 2021
\(11x^2-15x+4=0\)
\(\Leftrightarrow11x^2-11x-4x+4=0\)
\(\Leftrightarrow11x\left(x-1\right)-4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(11x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\11x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{4}{11}\end{matrix}\right.\)
\(S=\left\{1,\dfrac{4}{11}\right\}\)
20 tháng 2 2021
Đặt C(x)=0
\(\Leftrightarrow11x^2-15x+4=0\)
\(\Leftrightarrow11x^2-11x-4x+4=0\)
\(\Leftrightarrow11x\left(x-1\right)-4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(11x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\11x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\11x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{4}{11}\end{matrix}\right.\)
Vậy: Nghiệm của đa thức \(C\left(x\right)=11x^2-15x+4\) là 1 và \(\dfrac{4}{11}\)
31 tháng 3 2021
Ta có: x+y+1=0
nên x+y=-1
Ta có: \(N=x^2\left(x+y\right)-y^2\left(x+y\right)+x^2-y^2+2\left(x+y\right)+3\)
\(=\left(x+y\right)\left(x^2-y^2\right)+\left(x^2-y^2\right)+2\left(x+y\right)+3\)
\(=\left(x^2-y^2\right)\left(x+y+1\right)+2\left(x+y\right)+3\)
\(=\left(x^2-y^2\right)\cdot0+2\cdot\left(-1\right)+3\)
=-2+3=1
S
24 tháng 2
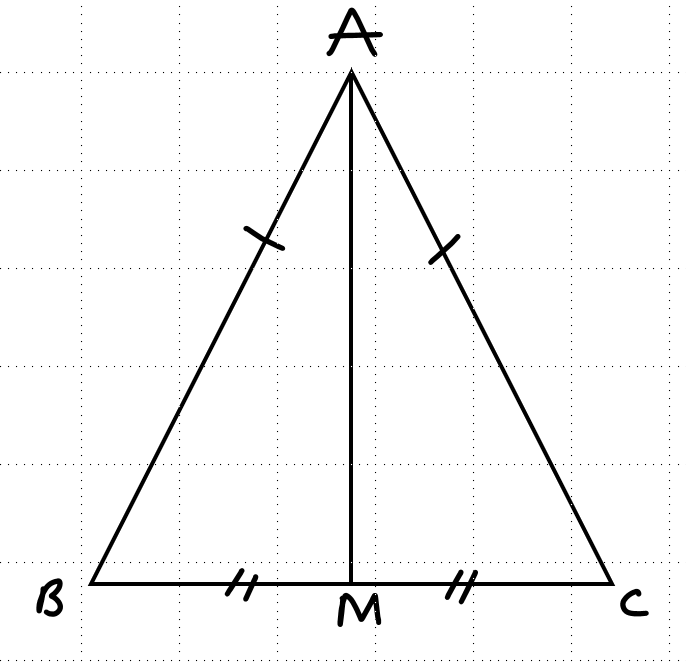
a. xét tam giác ABC có AB = AC (=17cm)
=> △ABC là △ cân tại A
lại có AM là đường trung tuyến
=> AM cũng là đường cao
=> AM vuông góc với BC
b. độ dài đoạn thẳng MB:
\(MB=\dfrac{1}{2}BC=\dfrac{1}{2}\cdot16=8\left(cm\right)\)
áp dụng định lý pythagore vào △BAM vuông tại M ta có:
\(AM=\sqrt{AB^2-BM^2}=\sqrt{17^2-8^2}=15\left(cm\right)\)
13 tháng 12 2020
Đáp án:
P=\(\frac{2}{3}\)
Giải thích các bước giải:
x:y:z=5:4:3
⇒ x5x5 =y4y4 ⇒y= 4x54x5
⇒ x5x5 =z3z3 ⇒z= 3x53x5
Thay vào biểu thức ta được:
P= x+2y−3zx−2y+3zx+2y−3zx−2y+3z= x+2.4x5−33x5x−2.4x5+33x5x+2.4x5−33x5x−2.4x5+33x5 =4x56x54x56x5 =2323
Vậy P=\(\frac{2}{3}\)
# Chúc bạn học tốt!
13 tháng 12 2020
Vì x,y,z tỉ lệ với các số 5,4,3 nên ta có : \(x:y:z=5:4:3\) hoặc \(\frac{x}{5}=\frac{y}{4}=\frac{z}{3}\)
Ta lại có : \(\frac{x}{5}=\frac{y}{4}=\frac{z}{3}=\frac{x}{5}=\frac{2y}{8}=\frac{3z}{9}\)
Đặt \(\frac{x}{5}=\frac{2y}{8}=\frac{3z}{9}=k\Rightarrow\hept{\begin{cases}x=5k\\2y=8k\\3z=9k\end{cases}}\)
\(P=\frac{x+2y-3z}{x-2y+3z}=\frac{5k+8k-9k}{5k-8k+9k}=\frac{4k}{6k}=\frac{4}{6}=\frac{2}{3}\)
Vậy \(P=\frac{2}{3}\)
NT
1
1.a)\(\left(x+4\right)^2+8=9\)
\(\Rightarrow\left(x+4\right)^2=1\)
\(\Rightarrow\orbr{\begin{cases}x+4=1\\x+4=-1\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x=-3\\x=-5\end{cases}}\)
Vậy ...
b)\(\left|x+6\right|=10\)
\(\Rightarrow\orbr{\begin{cases}x+6=10\\x+6=-10\end{cases}\Rightarrow}\orbr{\begin{cases}x=4\\x=-16\end{cases}}\)
Vậy ...
c)\(\frac{x+5}{8}+\frac{x-1}{14}+\frac{x-5}{18}+3=0\)
\(\Rightarrow\left(\frac{x+5}{8}+1\right)+\left(\frac{x-1}{14}+1\right)+\left(\frac{x-5}{18}+1\right)=0\)
\(\Rightarrow\frac{x+13}{8}+\frac{x+13}{14}+\frac{x+13}{18}=0\)
\(\Rightarrow\left(x+13\right)\left(\frac{1}{8}+\frac{1}{14}+\frac{1}{18}\right)=0\)
Dễ thấy : \(\frac{1}{8}+\frac{1}{14}+\frac{1}{18}>0\)
\(\Rightarrow x+13=0\)
\(\Rightarrow x=-13\)
Vậy ...
2.Từ \(\frac{a}{2}=\frac{b}{4}=\frac{c}{5}\),đặt \(\frac{a}{2}=\frac{b}{4}=\frac{c}{5}=k\)
\(\Rightarrow\hept{\begin{cases}a=2k\\b=4k\\c=5k\end{cases}}\Rightarrow abc=2k.4k.5k=40k^3=40\)
\(\Rightarrow k^3=1\Rightarrow k=1\)
\(\Rightarrow\hept{\begin{cases}a=2.1=2\\b=4.1=4\\c=5.1=5\end{cases}}\)
Vậy ...