K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 10 2016
bài 96 :
a) = \(\left(1\frac{4}{23}-\frac{4}{23}\right)\) + \(\left(\frac{5}{21}+\frac{16}{21}\right)\) + 0,5 = 1+1+0,5 = 2,5
b) = \(\frac{3}{7}\) \(\left(19\frac{1}{3}-33\frac{1}{3}\right)\)= \(\frac{3}{7}\) . (-14) = -6
c)= \(\frac{1}{3}\) \(\left[-\left(-\frac{1}{3}\right)^2.9+1\right]\) = \(\frac{1}{3}\) \(\left(-\frac{1}{9}.9+1\right)\) = \(\frac{1}{3}\) (-1+1) = \(\frac{0}{3}\) = 0
d)= \(\left(15\frac{1}{4}-25\frac{1}{4}\right)\): \(\left(-\frac{5}{7}\right)\) = (-10) : \(\left(-\frac{5}{7}\right)\) = 14
bài 97 :
a) = -6,37 . ( 0,4 . 2,5 ) = -6,37 . 1 = -6,37
b) = ( - 0,125 . 8 ) . (-5,3) = (-1) . (-5,3) = 5,3
c) = [ ( -2,5 ) . (-4) ] . (-7,9) = 10 . ( -7,9) = -79
d) = [ ( -0,375 ) . (-8) ] . \(\frac{13}{3}\) = 3.\(\frac{13}{3}\) = 13
bài 98 :
a) => y = \(\frac{21}{10}\) :\(\left(-\frac{3}{5}\right)\) => y = \(-\frac{7}{2}\)
b) => y = \(-\frac{64}{33}.\frac{3}{8}=-\frac{8}{11}\)
c) => \(\frac{7}{5}y\) = \(-\frac{4}{5}-\frac{3}{7}\) => \(\frac{7}{5}y\) = \(-\frac{43}{35}\) => y = \(-\frac{43}{35}:\frac{7}{5}\) = \(-\frac{43}{49}\)
d) => \(-\frac{11}{12}y=\frac{5}{6}-\frac{1}{4}\Rightarrow-\frac{11}{12}y=\frac{7}{12}\Rightarrow y=-\frac{7}{11}\)
27 tháng 10 2016
bài 103 :
gọi a , b là tiền lãi mà mỗi tổ chức được chia ( a, b \(\in\) Z*) ta có :
\(\frac{a}{3}=\frac{b}{5}\) và a+b = 12800000
Từ \(\frac{a}{3}=\frac{b}{5}\)
Áp dụng tính chất của dãy tỉ số bằng nhau :
\(\Rightarrow\frac{a}{3}=\frac{b}{5}=\frac{a+b}{3+5}=\frac{12800000}{8}=1600000\)
vậy \(\frac{a}{3}=1600000\Rightarrow a=4800000\)
\(\frac{b}{5}=1600000\Rightarrow b=8000000\)
( thỏa mãn điều kiện )
Tiền lãi mà các tổ chức đã được chia là 4800000 đồng và 8000000 đồng
bài 104 :
sau khi bán , tấm thứ 1 còn \(\frac{1}{2}\) , tấm thứ 2 còn \(\frac{1}{3}\) , tấm thứ 3 còn \(\frac{1}{4}\)
Gọi chiều dài các tấm theo thứ tự là x, y , z ( x,y,z \(\in\) Z* ) , ta có :
\(\frac{1}{2}x=\frac{1}{3}y=\frac{1}{4}z\Rightarrow\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{x+y+z}{2+3+4}=\frac{108}{9}=12\)
Vậy \(\frac{x}{2}=12\Rightarrow x=24\left(m\right)\)
\(\frac{y}{3}=12\Rightarrow y=36\left(m\right)\)
\(\frac{z}{4}=12\Rightarrow z=48\left(m\right)\)
( thỏa mãn điều kiện )
Chiều dài mỗi tấm vải lúc bạn đầu lần lượt là 24(m) , 36(m) , 48(m)
bài 105 :
a) ta có \(\sqrt{0,01}=0,1;\sqrt{0,25}=0,5\)
vậy \(\sqrt{0,01}-\sqrt{0,25}=0,1-0,5=-0,4\)
b) \(\sqrt{100}=10\Rightarrow0,5\sqrt{100}=0,5.10=5\)
\(\sqrt{\frac{1}{4}}=\sqrt{0,25}=0,5\)
vậy \(0,5\sqrt{100}-\sqrt{\frac{1}{4}}=5-0,5=4,5\)
~~Chúc bạn học tốt
30 tháng 7 2021
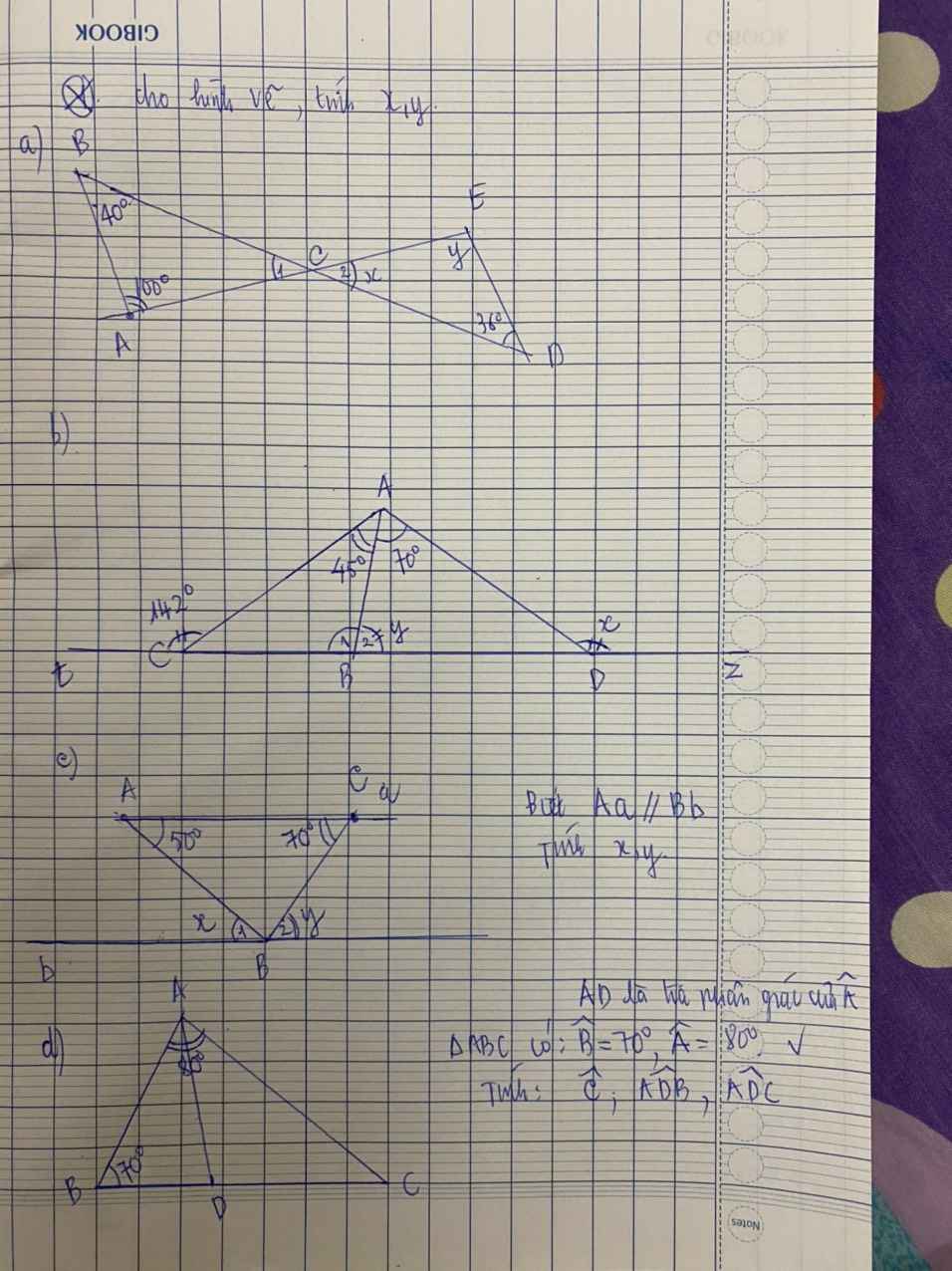
a,\(=>\angle\left(C1\right)=x=180-40-100=40^o\)
\(=>y=\angle\left(E\right)=180-40-36=104^o\)
b,\(y=180-[45+\left(180-142\right)]=97^o\)
\(=>x=70+97=167^o\)
c,\(x=\angle\left(A\right)=50^o\left(so-le-trong\right)\)
\(y=\angle\left(C\right)=70^O\left(so-le-trong\right)\)
d,\(\angle\left(C\right)=180-80-70=30^o\)
AD phân giác \(=>\angle\left(BAD\right)=\angle\left(CAD\right)=\dfrac{80}{2}=40^o\)
\(=>\angle\left(ADB\right)=180-(70+\dfrac{80}{2})=70^o\)
\(=>\angle\left(ADC\right)=180-70=110^o\)
21 tháng 10 2016
Bài 2:
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow\begin{cases}a=kb\\c=kd\end{cases}\)
=> \(\frac{5a+3b}{5a-3b}=\frac{5kb+3b}{5kb-3b}=\frac{b\left(5k+3\right)}{b\left(5k-3\right)}=\frac{5k+3}{5k-3}\left(1\right)\)
\(\frac{5c+3d}{5c-3d}=\frac{5kd+3d}{5kd-3d}=\frac{d\left(5k+3\right)}{d\left(5k-3\right)}=\frac{5k+3}{5k-3}\left(2\right)\)
Từ (1) và (2) => \(\frac{5a+3b}{5a-3b}=\frac{5c+3d}{5c-3d}\)
21 tháng 10 2016
Bài 3:
Đặt \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=k\)
=> \(\frac{a}{b}.\frac{b}{c}.\frac{c}{d}=k^3\)
=> \(\frac{a}{d}=k^3\) (1)
Lại có: \(\frac{a+b+c}{b+c+d}=\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=k\)
=> \(\left(\frac{a+b+c}{b+c+d}\right)^3=k^3\) (2)
Từ (1) và (2) => \(\frac{a}{d}=\left(\frac{a+b+c}{b+c+d}\right)^3\)
24 tháng 6 2023
a: Xét ΔABI vuông tại I và ΔACI vuông tại I có
AB=AC
AI chung
=>ΔABI=ΔACI
b: Sửa đề: cắt BK tại D
Xét ΔKAD vàΔKCB có
góc KAD=góc KCB
KA=KC
góc AKD=góc CKB
=>ΔKAD=ΔKCB
=>AD=CB
mà AD//CB
nên ABCD là hình bình hành
=>AB=CD
Bài 2:
2: \(\left\{{}\begin{matrix}2a=7c\\2b=5c\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{7}=\dfrac{c}{2}\\\dfrac{b}{5}=\dfrac{c}{2}\end{matrix}\right.\Leftrightarrow\dfrac{a}{7}=\dfrac{b}{5}=\dfrac{c}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{7}=\dfrac{b}{5}=\dfrac{c}{2}=\dfrac{a+2b-c}{7+2\cdot5-2}=\dfrac{30}{15}=2\)
Do đó: a=14; b=10; c=4