làm giúp mk vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
2
25 tháng 8 2018
có 2 cách bạn ạ
Ta thấy mỗi số hạng của tổng trên là tích của hai số tự nhên liên tiếp, khi đó:
Gọi a1 = 1.2 → 3a1 = 1.2.3 → 3a1 = 1.2.3 - 0.1.2
a2 = 2.3 → 3a2 = 2.3.3 → 3a2 = 2.3.4 - 1.2.3
a3 = 3.4 → 3a3 = 3.3.4 → 3a3 = 3.4.5 - 2.3.4
…………………..
an-1 = (n - 1)n → 3an-1 =3(n - 1)n → 3an-1 = (n - 1)n(n + 1) - (n - 2)(n - 1)n
an = n(n + 1) → 3an = 3n(n + 1) → 3an = n(n + 1)(n + 2) - (n - 1)n(n + 1)
Cộng từng vế của các đẳng thức trên ta có:
3(a1 + a2 + … + an) = n(n + 1)(n + 2)
học tốt
25 tháng 8 2018
cách 2
Ta có
3A = 1.2.3 + 2.3.3 + … + n(n + 1).3 = 1.2.(3 - 0) + 2.3.(3 - 1) + … + n(n + 1)[(n - 2) - (n - 1)] = 1.2.3 - 1.2.0 + 2.3.3 - 1.2.3 + … + n(n + 1)(n + 2) - (n - 1)n(n + 1) = n(n + 1)(n + 2) 
* Tổng quát hoá ta có:
k(k + 1)(k + 2) - (k - 1)k(k + 1) = 3k(k + 1). Trong đó k = 1; 2; 3; …
Ta dễ dàng chứng minh công thức trên như sau:
k(k + 1)(k + 2) - (k - 1)k(k + 1) = k(k + 1)[(k + 2) - (k - 1)] = 3k(k + 1)
tham khảo trên mạng có cả !!
mk vs ạ
8 tháng 8 2023
Mình xin phép bổ sung một chút vào trong hình vẽ nha bạn. Chứ để như vậy thì ko chứng minh a song song với b đâu
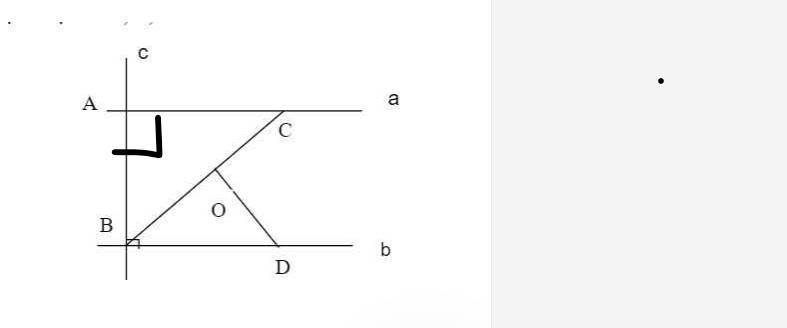
a: a vuông góc AB
b vuông góc AB
=>a//b
b: a//b
=>góc ACB=góc CBD
=>góc CBD=40 độ
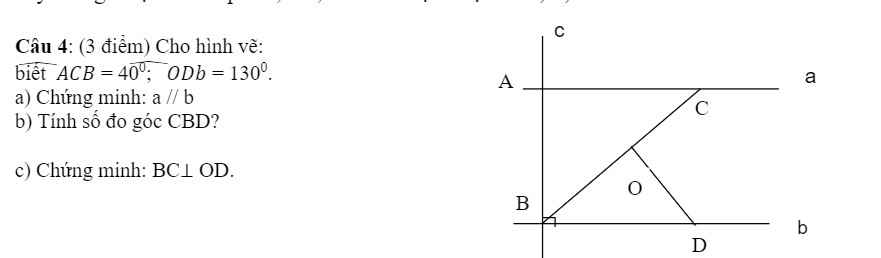
c: góc ODB=180-130=50 độ
góc ODB+góc OBD=50+40=90 độ
=>ΔOBD vuông tại O
=>DO vuông góc BC
12 tháng 9 2018
Tiến hành phân bổ bình quân theo tỷ lệ thuận số người mỗi đội, ta có
Số dụng cụ đội 1: 108/(10+12+5) x 10 = 40
Số dụng cụ đội 2: 108/(10+12+5)x12 = 48
Số dụng cụ đội 3: 108/(10+12+5)x5 = 20
giúp mk vs mk cảm ơn ạ
27 tháng 6 2023
Gọi số bi của Vương là x
Số bi trong mỗi hộp loại 1 là x/9
Số bi trong mỗi hộp loại 2 là x/6
Theo đề, ta có: x/6-x/9=4
=>x/18=4
=>x=72
HG
1
PL
1
9 tháng 2 2022
a: Đặt a/b=c/d=k
=>a=bk; c=dk
\(\dfrac{7a^2+3ab}{11a^2-8b^2}=\dfrac{7\cdot b^2k^2+3\cdot bk\cdot b}{11\cdot b^2k^2-8\cdot b^2}=\dfrac{b^2k\left(7k+3\right)}{b^2\left(11k^2-8\right)}=\dfrac{k\left(7k+3\right)}{11k^2-8}\)
\(\dfrac{7c^2+3cd}{11c^2-8d^2}=\dfrac{7\cdot d^2k^2+3\cdot dk\cdot d}{11\cdot d^2k^2-8d^2}=\dfrac{k\left(7k+3\right)}{11k^2-8}\)
Do đó: \(\dfrac{7a^2+3ab}{11a^2-8b^2}=\dfrac{7c^2+3cd}{11c^2-8d^2}\)
c: \(\dfrac{3a+2c}{3b+2d}=\dfrac{3bk+2dk}{3b+2d}=k\)
\(\dfrac{a}{b}=\dfrac{bk}{b}=k\)
Do đó: \(\dfrac{a}{b}=\dfrac{3a+2c}{3b+2d}\)