
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


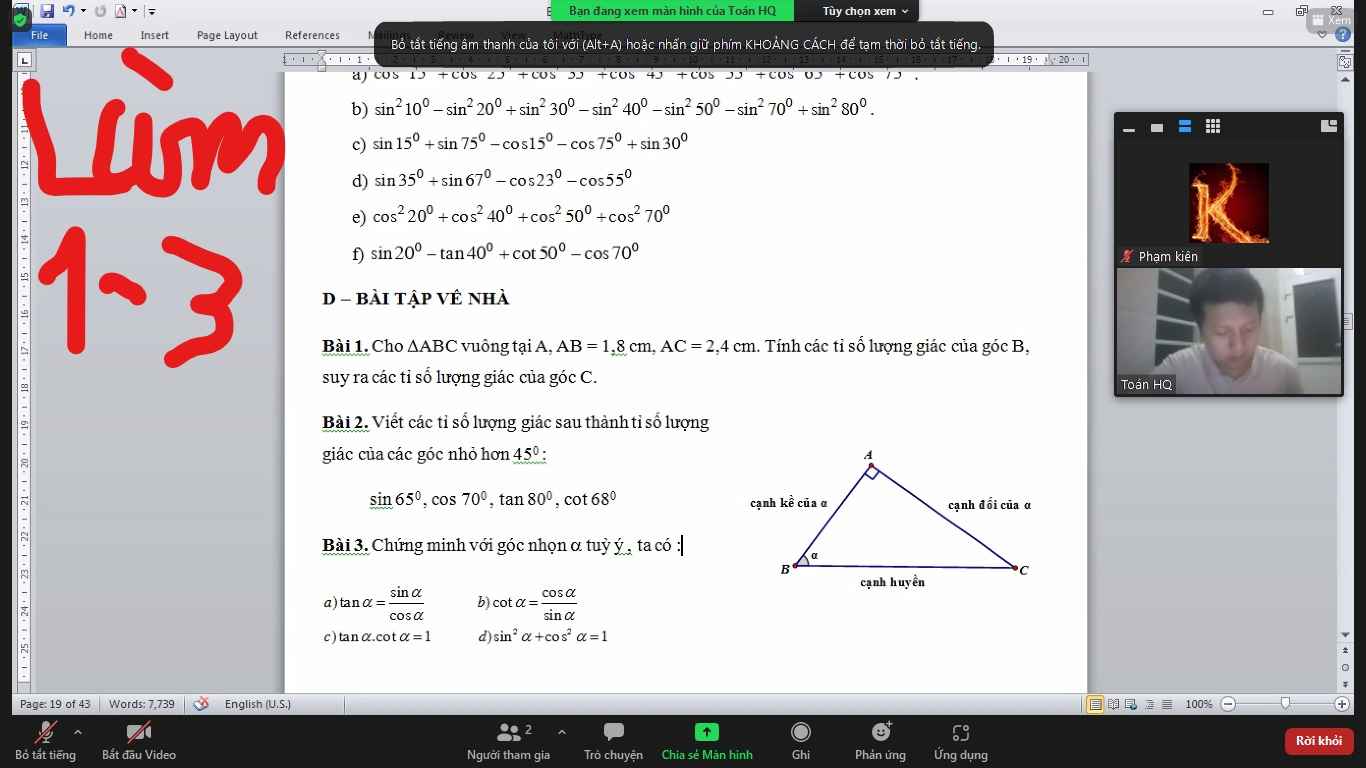
sin 650=cos 350
\(cos70^0=sin30^0\)
\(tan80^0=cot20^0\)
\(cot68^0=tan32^0\)


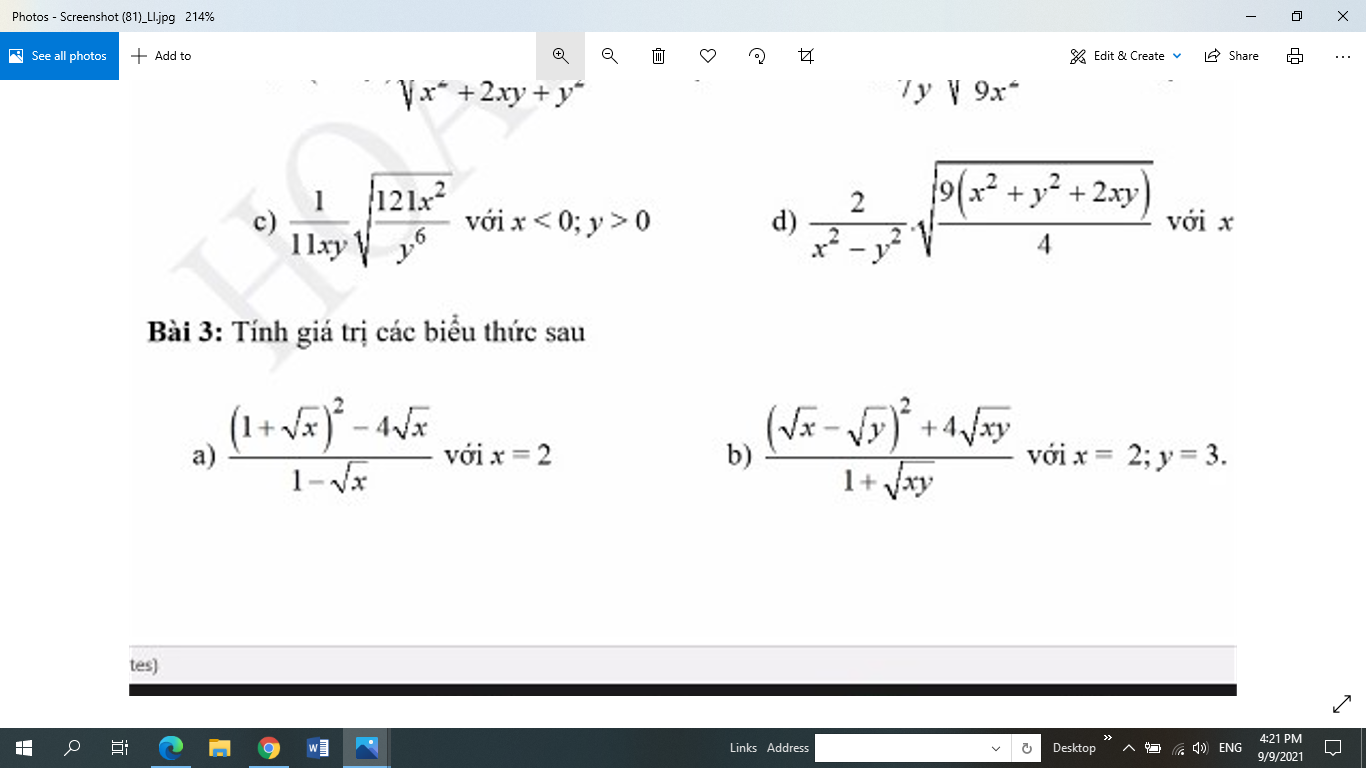
\(3,\\ a,\dfrac{\left(1+\sqrt{x}\right)^2-4\sqrt{x}}{1-\sqrt{x}}\\ =\dfrac{\sqrt{x}-2\sqrt{x}+1}{1-\sqrt{x}}=\dfrac{\left(1-\sqrt{x}\right)^2}{1-\sqrt{x}}=1-\sqrt{x}=1-\sqrt{2}\)
\(b,\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+4\sqrt{xy}}{1+\sqrt{xy}}\\ =\dfrac{x+2\sqrt{xy}+y}{1+\sqrt{xy}}=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{1+\sqrt{xy}}\\ =\dfrac{\left(\sqrt{2}+\sqrt{3}\right)^2}{1+\sqrt{6}}=\dfrac{5+2\sqrt{6}}{1+\sqrt{6}}\\ =\dfrac{\left(5+2\sqrt{6}\right)\left(\sqrt{6}-1\right)}{5}\\ =\dfrac{3\sqrt{6}+7}{5}\)

x^2 + x - 2 = 0
<=> ( x^2 - x ) + ( 2x - 2 ) = 0
<=> x . ( x - 1 ) + 2 . ( x - 1 ) = 0
<=> ( x - 1 ) . ( x + 2 ) = 0
<=> x - 1 = 0 hoặc x + 2 = 0
<=> x = 1 hoặc x = -2
Vậy .......
Tk mk nha

a. Giả sử: \(3+\sqrt{12}>\sqrt{16}\)
<=> \(\sqrt{12}>1\) (thỏa mãn)
Vậy \(3+\sqrt{12}>\sqrt{16}\)
b. \(4\sqrt{7}=\sqrt{4^2.7}=\sqrt{112}\)
\(3\sqrt{13}=\sqrt{3^2.13}=\sqrt{117}\)
Ta thấy: 112 < 117
Vậy \(4\sqrt{7}< 3\sqrt{13}\)

7a) \(\Delta=\left(3m+1\right)^2-4\left(2m^2+m-1\right)=m^2+2m+5=\left(m+1\right)^2+4>0\)
\(\Rightarrow\) pt luôn có 2 nghiệm phân biệt
b) Áp dụng hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=3m+1\\x_1x_2=2m^2+m-1\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2-3x_1x_2=\left(x_1+x_2\right)^2-5x_1x_2=\left(3m+1\right)^2-5\left(2m^2+m-1\right)\)
\(=-m^2+m+6=-\left(m^2-m-6\right)\)
Ta có: \(m^2-m-6=m^2-2.m.\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2-\dfrac{25}{4}\)
\(=\left(m-\dfrac{1}{2}\right)^2-\dfrac{25}{4}\ge-\dfrac{25}{4}\Rightarrow-\left(m^2-m-6\right)\le\dfrac{25}{4}\)
\(\Rightarrow GTLN=\dfrac{25}{4}\) khi \(m=\dfrac{1}{2}\)
a) Ta có: \(x^2-\left(3m+1\right)x+2m^2+m-1\)
\(\Delta=\left(3m+1\right)^2-4\left(2m^2+m-1\right)\)
\(=9m^2+6m+1-8m^2-4m+4\)
\(=m^2+2m+5\)
\(=\left(m+1\right)^2+4>0\forall m\)
Do đó: Phương trình luôn có hai nghiệm phân biệt với mọi m
b) Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=3m+1\\x_1x_2=2m^2+m-1\end{matrix}\right.\)
Ta có: \(B=x_1^2+x_2^2-3x_1x_2\)
\(=\left(x_1+x_2\right)^2-5x_1x_2\)
\(=\left(3m+1\right)^2-5\left(2m^2+m-1\right)\)
\(=9m^2+6m+1-10m^2-5m+5\)
\(=-m^2+m+6\)
\(=-\left(m^2-m-6\right)\)
\(=-\left(m^2-2\cdot m\cdot\dfrac{1}{2}+\dfrac{1}{4}\right)+\dfrac{25}{4}\)
\(=-\left(m-\dfrac{1}{2}\right)^2+\dfrac{25}{4}\le\dfrac{25}{4}\forall m\)
Dấu '=' xảy ra khi \(m=\dfrac{1}{2}\)

\(P=\dfrac{a^2+\sqrt{a}}{a-\sqrt{a}+1}-\dfrac{2a+\sqrt{a}}{\sqrt{a}}+1\) (Đk:\(a>0\))
\(=\dfrac{\sqrt{a}\left(a\sqrt{a}+1\right)}{a-\sqrt{a}+1}-\dfrac{\sqrt{a}\left(2\sqrt{a}+1\right)}{\sqrt{a}}+1\)
\(=\sqrt{a}\left(\sqrt{a}+1\right)-2\sqrt{a}-1+1\)
\(=a-\sqrt{a}\)
b) \(P=2\Leftrightarrow a-\sqrt{a}=2\Leftrightarrow a-\sqrt{a}-2=0\)\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{a}=2\\\sqrt{a}=-1\left(vn\right)\end{matrix}\right.\)\(\Rightarrow a=4\) (tm)
Vậy a=4 thì P=2
c) \(P=a-\sqrt{a}=\left(\sqrt{a}-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)
Dấu "=" xảy ra khi \(\sqrt{a}=\dfrac{1}{2}\Leftrightarrow a=\dfrac{1}{4}\)
Vậy \(P_{min}=-\dfrac{1}{4}\)
Coi pt \(a-\sqrt{a}-2=0\) là pt ẩn \(\sqrt{a}\)
Hoặc e đặt \(t=\sqrt{a}\)
Pt tt: \(t^2-t-2=0\) \(\Leftrightarrow\left[{}\begin{matrix}t=-1\\t=2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{a}=-1\\\sqrt{a}=2\end{matrix}\right.\)

Đầu tiên ta bình phương tất cả:
\(\sqrt{3^2}=3\)
\(5^2=25\)
\(\sqrt{8^2}=8\)
Sau khi bình phương ta có:
3 ... 25 - 8
3 < 17
=> \(\sqrt{3}< 5-\sqrt{8}\)



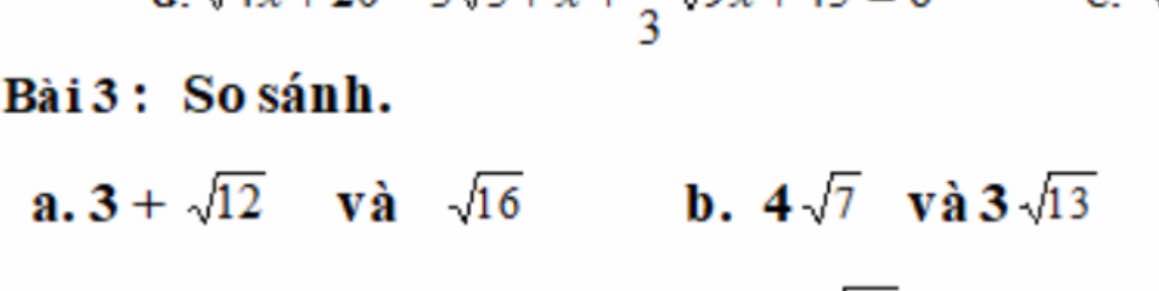


a) Ta có: \(P=\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}+\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}-1\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}-\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}+1\right)\)
\(=\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{ab}-1\right)+\left(\sqrt{ab}+\sqrt{a}\right)\left(\sqrt{ab}+1\right)-\left(ab-1\right)}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}:\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{ab}-1\right)-\left(\sqrt{ab}+\sqrt{a}\right)\left(\sqrt{ab}+1\right)+ab-1}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}\)
\(=\dfrac{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1+ab+\sqrt{ab}+a\sqrt{b}+\sqrt{a}-ab+1}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}:\dfrac{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1-ab-\sqrt{ab}-a\sqrt{b}-\sqrt{a}+ab-1}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}\)
\(=\dfrac{2a\sqrt{b}+2\sqrt{ab}}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}\cdot\dfrac{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}{-2\sqrt{a}-2}\)
\(=\dfrac{2\sqrt{ab}\left(\sqrt{a}+1\right)}{-2\left(\sqrt{a}+1\right)}\)
\(=-\sqrt{ab}\)
b) Ta có: \(b=\dfrac{\sqrt{3}-1}{\sqrt{3}+1}\)
\(=\dfrac{\left(\sqrt{3}-1\right)^2}{2}\)
\(=\dfrac{4-2\sqrt{3}}{2}=2-\sqrt{3}\)
Thay \(a=2+\sqrt{3}\) và \(b=2-\sqrt{3}\) vào P, ta được:
\(P=-\sqrt{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}=-1\)