K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VN
1
14 tháng 12 2018
\(\left(2119-x\right)\cdot2,23=174\)
\(\Rightarrow219-x=\frac{174}{2,23}\)
\(x=219-\frac{174}{2,23}\)
DM
Các bạn giúp mik làm bài 12 nha mik đang cần gấp chỉ cần làm trắc nghiệm thui nha
2
4 tháng 1 2022
Số học sinh khá là:
\(800\times60\%=480\left(học.sinh\right)\)
Số học sinh giỏi là:
\(800\times13\%=104\left(học.sinh\right)\)
Số học trung bình là:
\(800\times17\%=136\left(học.sinh\right)\)
Số học yếu là:
\(800-480-104-136=80\left(học.sinh\right)\)
4 tháng 1 2022
Bài 4:
Số học sinh khá là:
800x60%=480(bạn)
Số học sinh giỏi là:
800x13%=104(bạn)
Số học sinh trung bình là:
800x17%=136(bạn)
Số học sinh yếu là
800-480-104-136=80(bạn)
14 tháng 12 2021
Bài 326:
\(=\left(1+\dfrac{1}{2}\right)+\left(1+\dfrac{1}{6}\right)+...+\left(1+\dfrac{1}{90}\right)\\ =\left(1+1+...+1\right)+\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{9.10}\right)\\ =9+\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\right)\\ =9+\left(1-\dfrac{1}{10}\right)=9+\dfrac{9}{10}=\dfrac{99}{10}\)
NT
1
15 tháng 1 2023
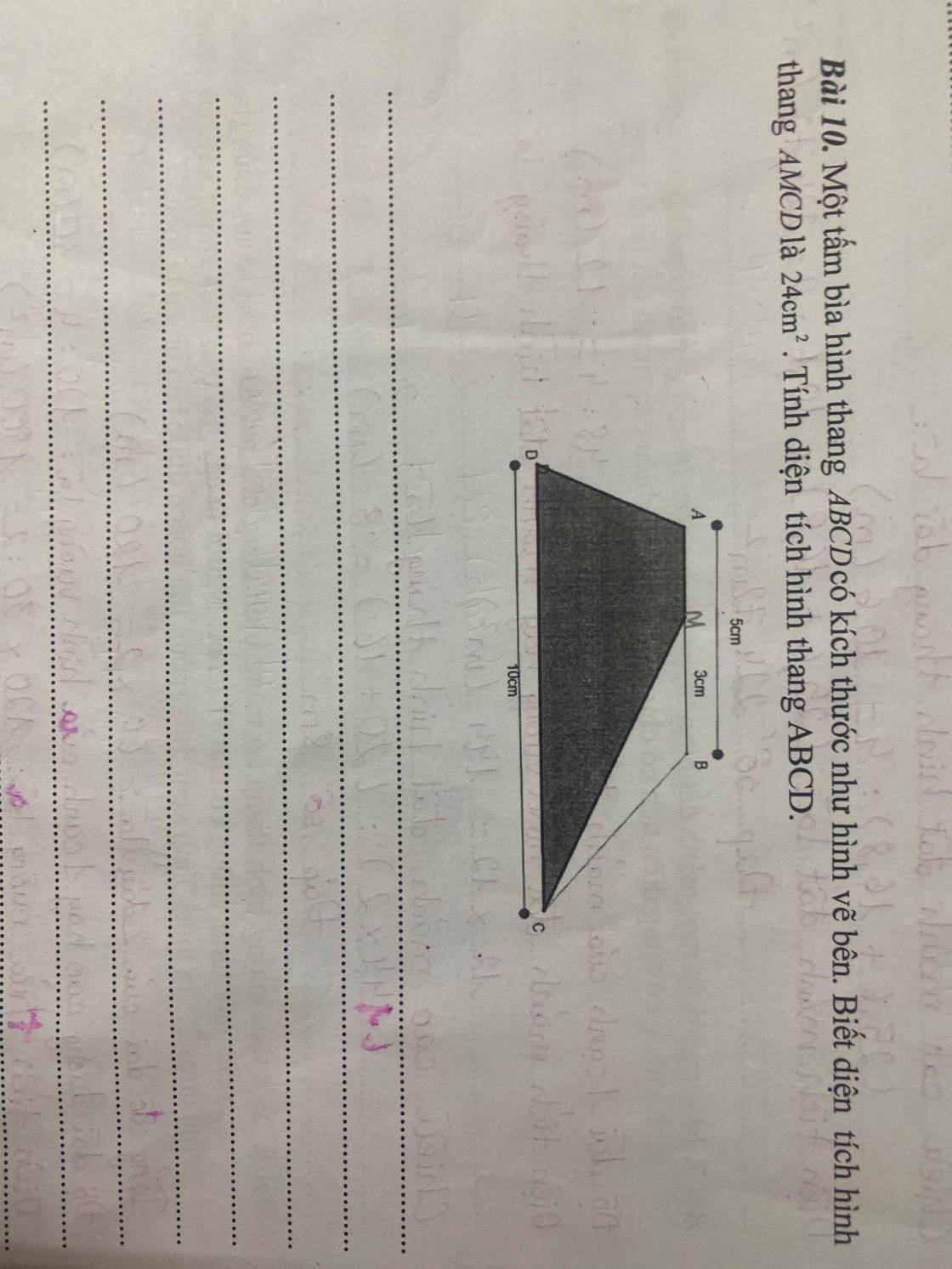
\(Cạnh\) \(AM\) = \(AB-MB\) = \(5-3\text{=}2\)cm
Đường cao của hình thang AMCD là : \(S_{AMCD}.2:\left(AM+CD\right)\)
\(\Rightarrow\) Đường cao của hình thang AMCD = \(24.2:\left(2+10\right)\text{=}4\)cm ( gọi là AH )
\(\Rightarrow\) Diện tích hình thang ABCD = \(\dfrac{\left(AB+CD\right).AH}{2}\)=\(\dfrac{\left(5+10\right).4}{2}\) = 30 cm2
2 tháng 7 2023
5:
a: Chiều rộng là 18*1/6=3m
S=18*3=54m2
Số viên gạch cần mua là:
54*10^4:30^2=600 viên
b: Số viên gạch phải giảm đi là:
600*5/6=500 viên
NT
1
10 tháng 3 2022
Sau khi phơi còn lại số thóc là:
780 – 130 = 650 (kg)`
Lượng nước trong 650 kg thóc tươi là:
650 : 100 × 25 = 162,5 (kg)`
Lượng thóc thuần hạt trong 650 kg thóc tươi là:
650 – 162,5 = 487,5 (kg)
Lượng nước còn lại trong thóc sau khi phơi là:
650 – 487,5 = 162,5 (kg)
Tỉ số % giữa lượng nước và lượng thuần hạt có trong thóc đã phơi là:
162,5 : 487,5 × 100 = 33,33%
Đáp số: 33,33%
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
2 tháng 6 2023
A = \(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\)+ \(\dfrac{1}{16}\) + \(\dfrac{1}{32}\) + \(\dfrac{1}{64}\)+......+\(\dfrac{1}{1024}\)
A \(\times\)2 = 1 + \(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\) + \(\dfrac{1}{16}\) + \(\dfrac{1}{32}\)+\(\dfrac{1}{64}\)+...+\(\dfrac{1}{512}\)
A\(\times\)2 - A = 1 - \(\dfrac{1}{1024}\)
A = \(\dfrac{1023}{1024}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
2 tháng 6 2023
B = \(\dfrac{1}{1\times2}\)+\(\dfrac{1}{2\times3}\)+\(\dfrac{1}{3\times4}\)+\(\dfrac{1}{4\times5}\)+...+\(\dfrac{1}{98\times99}\)+\(\dfrac{1}{99\times100}\)
B = \(\dfrac{1}{1}\) - \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\)+ \(\dfrac{1}{3}\)-\(\dfrac{1}{4}\)+\(\dfrac{1}{4}\)-\(\dfrac{1}{5}\)+...+\(\dfrac{1}{98}\)-\(\dfrac{1}{99}\)+\(\dfrac{1}{99}\)-\(\dfrac{1}{100}\)
B = 1 - \(\dfrac{1}{100}\)
B = \(\dfrac{99}{100}\)