Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
+ Số chỉnh hợp chập k của n phần tử:
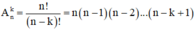
+ Số tổ hợp chập k của n phần tử:
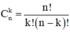
+ Ví dụ:
- Số chỉnh hợp chập 3 của 5: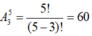 
- Số tổ hợp chập 3 của 5: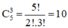 
- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau để cắm vào 5 lọ khác nhau:
⇒ Có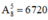 
cách chọn.
- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau
⇒ Có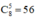 
cách chọn.
Chỉnh hợp chập k của n phần tử là một tập hợp con k phần tử của một tập hợp n phần tử được sắp xếp theo một thứ tự nào đó.
Tổ hợp chập k của n phần tử là tập hợp con k phần tử của một tập hợp n phần tử không để ý đến thứ tự các phần tử của tập hợp con đó.
Số tập hợp con có k phần tử của tập hợp A (có 18 phần tử)
\(C_{18}^k\left(k=1,.....,18\right)\)
Để tìm max \(C_{18}^k,k\in\left\{1,2,.....,18\right\}\) (*), ta tiến hành giải bất phương trình sau :
\(\frac{C_{18}^k}{C_{18}^{k+1}}< 1\)
\(\Leftrightarrow C_{18}^k< C_{18}^{k+1}\)
\(\Leftrightarrow\frac{18!}{\left(18-k\right)!k!}< \frac{18!}{\left(17-k\right)!\left(k+1\right)!}\)
\(\Leftrightarrow\left(18-k\right)!k!>\left(17-k\right)!\left(k+1\right)!\)
\(\Leftrightarrow17>2k\)
\(\Leftrightarrow k< \frac{17}{2}\)
Điều kiện (*) nên k = 1,2,3,.....8
Suy ra \(\frac{C_{18}^k}{C_{18}^{k+1}}>1\) khi k = 9,10,...,17
Vậy ta có
\(C^1_{18}< C_{18}^2< C_{18}^3< .........C_{18}^8< C_{18}^9>C_{18}^{10}>.....>C_{18}^{18}\)
Vậy \(C_{18}^k\) đạt giá trị lớn nhất khi k = 9. Như thế số tập hợp con gồm 9 phần tử của A là số tập hợp con lớn nhất.
|
Cho tập hợp A có n phần tử (n ≥ 1) |
||
|
Chỉnh hợp chập k của n phần tử |
Sắp xếp thứ tự các phần tử |
_ Sử dụng k phần tử trong số n phần tử của A (k ≤ n) và sắp xếp thứ tự k phần tử này (mỗi cách sắp xếp là một chỉnh hợp chập k của phần tử) _ Số chỉnh hợp chập k của n phần tử là:\(A^k_n=\dfrac{n!}{\left(n-k\right)!}\)
|
|
Tổ hợp chập k của n phần tử |
Không chú ý đến thứ tự của các phần tử |
_ Sử dụng k phần tử trong n phần tử A (k ≤ n) và không để ý đến thứ tự của các phần tử này. _Số tổ hợp chập k của n phần tử là: \(C^k_n=\dfrac{n!}{k!\left(n-k\right)!}\)
|
Chọn B
Ta có số chỉnh hợp chập k của một tập hợp gồm n phần tử là: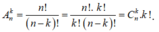 
.
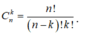
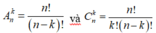
Chọn B