Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số tập con 4 phần tử bằng 20 lần số tập con 2 phần tử
\(\Rightarrow C_n^4=20C_n^2\) \(\Rightarrow n=18\)
Số tập con gồm k phần tử: \(C_{18}^k\)
Để số tập con gồm k phần tử đạt max:
\(\Leftrightarrow\left\{{}\begin{matrix}C_{18}^k\ge C_{18}^{k+1}\\C_{18}^k\ge C_{18}^{k-1}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\frac{18!}{\left(18-k\right)!.k!}\ge\frac{18!}{\left(17-k\right)!\left(k+1\right)!}\\\frac{18!}{\left(18-k\right)!k!}\ge\frac{18!}{\left(19-k\right)!\left(k-1\right)!}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}k+1\ge18-k\\19-k\ge k\end{matrix}\right.\) \(\Rightarrow k=9\)

Đáp án D
Số tập con của A có 8 phần tử C n 8
và số tập của A có 4 phần tử là C n 4
⇒ 26 = C n 8 C n 4 = ( n - 7 ) ( n - 5 ) ( n - 4 ) 1680
⇔ n = 20
Số tập con gồm k phần tử là C 20 k
Khi xảy ra C 20 k > C 20 k + 1
![]()
Vậy với k = 10 thì C 20 k đạt giá trị nhỏ nhất.

Chọn A
Ta lấy 4 phần tử bất kì trong tập hợp gồm 9 phần tử có C 9 4 cách.
Vậy số tập con gồm 4 phần tử là C 9 4

1/ Số cách chọn 4 học sinh bất kì: \(C_{12}^4\)
Số cách chọn 4 học sinh có mặt đủ 3 lớp:
\(C_5^2.C_4^1.C_3^1+C_5^1.C_4^2.C_3^1+C_5^1.C_4^1.C_3^2\)
Số cách chọn thỏa mãn yêu cầu:
\(C_{12}^4-\left(C_5^2.C_4^1.C_3^1+C_5^1.C_4^2.C_3^1+C_5^1.C_4^1.C_3^2\right)\)
2/ Số tập con có 2 phần tử: \(C_n^2\)
Số tập con có 4 phần tử: \(C_n^4\)
\(C_n^4=20C_n^2\Leftrightarrow\frac{n!}{\left(n-4\right)!.4!}=\frac{20n!}{\left(n-2\right)!.2!}\)
\(\Leftrightarrow\left(n-2\right)\left(n-3\right)=\frac{20.4!}{2!}=240\)
\(\Leftrightarrow n^2-5n-234=0\Rightarrow n=18\)
3/ Từ 10 chữ số {0;1;...;9} có \(C_{10}^3\) cách chọn bộ 3 số tự nhiên phân biệt
Với mỗi bộ số có duy nhất 1 cách sắp xếp thỏa mãn \(a>b>c\)
Vậy có \(C_{10}^3\) chữ số thỏa mãn

Đáp án C
Ta tìm số cặp số (a;b) thoả mãn
![]()
![]()
Có 49 cặp (a;b) thỏa mãn. Do đó S gồm 49 phần tử:
Ta tìm số cặp (a;b) thoả mãn
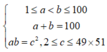
![]()
Do đó 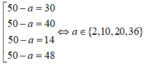
Vậy có 4 cặp số (a;b)có tổng bằng 100 và tích của chúng là một số chính phương.
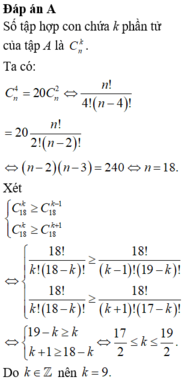



Số tập hợp con có k phần tử của tập hợp A (có 18 phần tử)
\(C_{18}^k\left(k=1,.....,18\right)\)
Để tìm max \(C_{18}^k,k\in\left\{1,2,.....,18\right\}\) (*), ta tiến hành giải bất phương trình sau :
\(\frac{C_{18}^k}{C_{18}^{k+1}}< 1\)
\(\Leftrightarrow C_{18}^k< C_{18}^{k+1}\)
\(\Leftrightarrow\frac{18!}{\left(18-k\right)!k!}< \frac{18!}{\left(17-k\right)!\left(k+1\right)!}\)
\(\Leftrightarrow\left(18-k\right)!k!>\left(17-k\right)!\left(k+1\right)!\)
\(\Leftrightarrow17>2k\)
\(\Leftrightarrow k< \frac{17}{2}\)
Điều kiện (*) nên k = 1,2,3,.....8
Suy ra \(\frac{C_{18}^k}{C_{18}^{k+1}}>1\) khi k = 9,10,...,17
Vậy ta có
\(C^1_{18}< C_{18}^2< C_{18}^3< .........C_{18}^8< C_{18}^9>C_{18}^{10}>.....>C_{18}^{18}\)
Vậy \(C_{18}^k\) đạt giá trị lớn nhất khi k = 9. Như thế số tập hợp con gồm 9 phần tử của A là số tập hợp con lớn nhất.