K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
3
2 tháng 10 2021
Bài 2:
\(\cos\alpha=\sqrt{1-\dfrac{4}{9}}=\dfrac{\sqrt{5}}{3}\)
\(\tan\alpha=\dfrac{2}{\sqrt{5}}=\dfrac{2\sqrt{5}}{5}\)
\(\cot\alpha=\dfrac{\sqrt{5}}{2}\)
LT
0
TK
1
GH
11 tháng 7 2023
\(cot\alpha=\dfrac{40}{9}\Rightarrow tan\alpha=\dfrac{1}{cot\alpha}=\dfrac{1}{\dfrac{40}{9}}=\dfrac{9}{40}\)
+) \(\dfrac{1}{cos^2\alpha}=1+tan^2\alpha\)
\(\Leftrightarrow\dfrac{1}{cos^2\alpha}=1+\left(\dfrac{9}{40}\right)^2\\ \Rightarrow cos\alpha=\sqrt{1:\left(1+\left(\dfrac{9}{40}\right)^2\right)}=\dfrac{40}{41}\)
+) \(sin^2\alpha=1-cos^2\alpha\)
\(\Leftrightarrow sin\alpha=\sqrt{1-cos^2\alpha}=\sqrt{1-\left(\dfrac{40}{41}\right)^2}=\dfrac{9}{41}\)
H9
HT.Phong (9A5)
CTVHS
6 tháng 10 2023
Bài 1:
a) Ta có:
\(tanB=\dfrac{AC}{AB}\Rightarrow\dfrac{AC}{AB}=\dfrac{5}{2}\)
\(\Rightarrow AC=\dfrac{AB\cdot5}{2}=\dfrac{6\cdot5}{2}=15\)
b) Áp dụng Py-ta-go ta có:
\(BC^2=AB^2+AC^2=6^2+15^2=261\)
\(\Rightarrow BC=\sqrt{261}=3\sqrt{29}\)
H9
HT.Phong (9A5)
CTVHS
6 tháng 10 2023
Bài 2:
\(\left\{{}\begin{matrix}sinM=sin40^o\approx0,64\Rightarrow cosN\approx0,64\\cosM=cos40^o\approx0,77\Rightarrow sinN\approx0,77\\tanM=tan40^o\approx0,84\Rightarrow cotN\approx0,84\\cotM=cot40^o\approx1,19\Rightarrow tanN\approx1,19\end{matrix}\right.\)
20 tháng 11 2023
Xét ΔABC vuông tại A có
\(sinB=sin56\simeq0,83\)
\(cosB=cos56\simeq0,56\)
\(tanB=tan56\simeq1,48\)
\(cotB=cot56\simeq0,67\)
Xét ΔABC vuông tại A có
\(cosC=sinB\simeq0,83\)
\(sinC=cosB\simeq-0,56\)
\(cotC=tanB=tan56\simeq1,48\)
\(tanC=cotB\simeq0,67\)
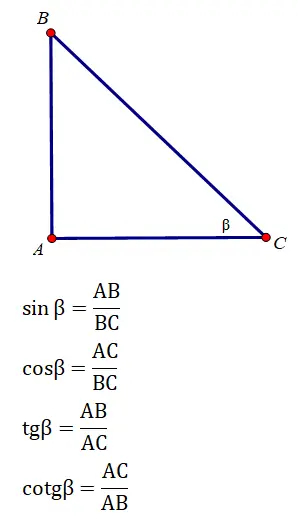
\(tana.cota=1\Rightarrow tana=\dfrac{1}{cota}=\dfrac{1}{\dfrac{40}{9}}=\dfrac{9}{40}\)
\(1+tan^2a=\dfrac{1}{cos^2a}=1+\left(\dfrac{9}{40}\right)^2=\dfrac{1681}{1600}\\ \Rightarrow cos^2a=\dfrac{1600}{1681}\\ \Rightarrow cosa=\dfrac{40}{41}\)
\(1+cot^2a=\dfrac{1}{sin^2a}=1+\left(\dfrac{40}{9}\right)^2=\dfrac{1681}{81}\\ \Rightarrow sin^2a=\dfrac{81}{1681}\\ \Rightarrow sina=\dfrac{9}{41}\)