Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức:
d(M0 ;∆) = \(\dfrac{\left|ax_0+by_0+c\right|}{\sqrt{a^2+b^2}}\)
a) d(M0 ;∆) = \(\dfrac{\left|4\cdot3+3\cdot5+1\right|}{\sqrt{4^2+3^2}}=\dfrac{28}{5}\)
b) d(B ;d) = \(\dfrac{\left|3\cdot1-4\cdot\left(-2\right)-26\right|}{\sqrt{3^2+\left(-4\right)^2}}=-\dfrac{15}{5}=\dfrac{15}{5}=3\)
c) Dễ thấy điểm C nằm trên đường thẳng m : C ε m

Áp dụng công thức:
d(M0 ;∆) =
a) d(M0 ;∆) = =
b) d(B ;d) = =
=
= 3
c) Dễ thấy điểm C nằm trên đường thẳng m : C ε m.

a) Khoảng cách từ điểm A đến \({\Delta _1}\) là: \(d\left( {A,{\Delta _1}} \right) = \frac{{\left| {3.1 - 1.\left( { - 2} \right) + 4} \right|}}{{\sqrt {{3^2} + {{\left( { - 1} \right)}^2}} }} = \frac{9}{{\sqrt {10} }}\)
b) Phương trình tổng quát của đường thẳng \({\Delta _2}\)là: \(2x + y + 3 = 0\)
Khoảng cách từ điểm B đến \({\Delta _2}\) là: \(d\left( {A,{\Delta _2}} \right) = \frac{{\left| {2.\left( { - 3} \right) + 1.2 + 3} \right|}}{{\sqrt {{2^2} + {1^2}} }} = \frac{1}{{\sqrt 5 }}\)

a) Khoảng cách từ \(M(1;2)\) đến \(\Delta :3x - 4y + 12 = 0\) là:
\(d\left( {M,\Delta } \right) = \frac{{\left| {3.1 - 4.2 + 12} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{7}{5}\)
b) \(\Delta \) có phương trình tham số \(\Delta :\left\{ \begin{array}{l}x = t\\y = - t\end{array} \right.\) nên có phương trình tổng quát là
\(\left( {x - 0} \right) + \left( {y - 0} \right) = 0 \Leftrightarrow x + y = 0\)
Suy ra khoảng cách từ điểm \(M(4;4)\) đến đường thẳng \(\Delta \) là
\(d\left( {M,\Delta } \right) = \frac{{\left| {1.4 + 1.4} \right|}}{{\sqrt {{1^2} + {1^2}} }} = 4\sqrt 2 \)
c) \(\Delta \) có phương trình tham số \(\Delta :\left\{ \begin{array}{l}x = t\\y = \frac{{ - 19}}{4}\end{array} \right.\) nên có phương trình tổng quát là
\(0.\left( {x - 0} \right) + \left( {y + \frac{{19}}{4}} \right) = 0 \Leftrightarrow y + \frac{{19}}{4} = 0\)
Suy ra khoảng cách từ điểm \(M(0;5)\) đến đường thẳng \(\Delta \) là
\(d\left( {M,\Delta } \right) = \frac{{\left| {5 + \frac{{19}}{4}} \right|}}{{\sqrt {{0^2} + {1^2}} }} = \frac{{39}}{4}\)
d) Khoảng cách từ \(M(0;0)\) đến \(\Delta :3x + 4y - 25 = 0\) là:
\(d\left( {M,\Delta } \right) = \frac{{\left| {3.0 + 4.0 - 25} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 5\)

a) Ta có: \(\Delta \):\(\frac{x}{{ - 4}} + \frac{y}{2} = 1 \Leftrightarrow x - 2y + 4 = 0\)
Vậy khoảng cách từ O đến \(\Delta \) là: \(d\left( {O;\Delta } \right) = \frac{{\left| {1.0 - 2.0 + 4} \right|}}{{\sqrt {{1^2} + {2^2}} }} = \frac{{4\sqrt 5 }}{5}\)
b) Lấy \(M\left( {0;1} \right) \in {\Delta _1}\)
Suy ra: \(d\left( {{\Delta _1},{\Delta _2}} \right) = d\left( {M,{\Delta _2}} \right) = \frac{{\left| {0 - 1 - 1} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \sqrt 2 \)

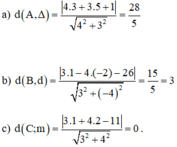
Khoảng cách từ điểm \(A\left( {1;1} \right)\) đến đường thẳng \(\Delta :3x + 4y + 13 = 0\) bằng:
\(d\left( {A,\Delta } \right) = \dfrac{{\left| {3.1 + 4.1 + 13} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 4\)
Chọn D