
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

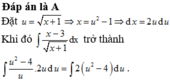

Câu 1.
A = {15;16;17;18;19} (0,25đ)
Câu 2.
a. 2.(72 – 2.32) – 60
= 2.(49 – 2.9) – 60 (0,25đ)
= 2.31 – 60 (0,25đ)
= 62 – 60 = 2 (0,25đ)
b. 27.63 + 27.37
= 27.(63 + 37) (0,25đ)
= 27.100 (0,25đ)
= 2700 (0,25đ)
c. l-7l + (-8) + l-11l + 2
= 7 + (-8) + 11 + 2 (0,5 đ)
= 12 (0,25đ)
d. 568 – 34 {5.l9 – ( 4-1)2l + 10}
= 568 – 34 {5.[9-9] + 10} (0,25đ)
= 568 – 34.10
= 568 – 340 (0,25đ)
= 228 (0,25đ)
Câu 3.
a)2x + 3 = 52 : 5
2x + 3 =5 (0,25đ)
2x = 5-3 (0,25đ)
2x =2 (0,25đ)
x=1 (0,25đ)
b)
105 – ( x + 7) = 27 : 25
105 – ( x + 7) = 22 (0,25đ)
105 – ( x + 7) = 4 (0,25đ)
x + 7 = 105 – 4 (0,25đ)
x + 7 = 101 (0,25đ)
x = 101 – 7 (0,25đ)
x = 94 (0,25đ)
Câu 4.
Gọi x (hs) là số học sinh lớp 6B phải tìm (30<x< 38, x)
Vì hs lớp 6B xếp 2, hàng, 4 hàng, 8 hàng đều vừa đủ nên x⋮2; x⋮4; x⋮8 hay x ∈ BC{2;4;8} (0,25đ)
Ta có: BCNN(2,4,8) = 8 (0,25đ)
⇒ BC(2,4,8) = B(8) ={0; 8; 16;24; 32; 40; …}
Mặt khác: 30<x< 38 (0,25đ)
Nên x = 32
Vậy số học sinh lớp 6B là 32 học sinh (0,25đ)
Câu 5.
Khi M nằm giữa và cách đều hai điểm A và B (0,5đ)
Vẽ được hình có điểm M là trung điểm của AB (0,5đ)
Câu 6.a)

0,25đ
Điểm A nằm giữa O và B (0,25đ)
Vì OA < OB ( 4 < 8 ) (0,25đ)
Ta có: AO + AB = OB
3 + AB = 6 (0,25đ)
AB = 6 -3 = 3 cm (0,25đ)
Vậy OA = AB = 3 cm (0,25đ)
b)
Vì A nằm giữa O, B và cách đều O và B ( OA = AB ) (0,25đ)
Nên A là trung điểm OB (0,25đ)

Đáp án B
Cách giải: A B → = - 1 ; - 2 ; 3
d:
x
-
2
1
=
y
-
1
-
2
=
z
-
1
2
có 1 VTCP
v
→
1
;
-
2
;
2
là một VTCP của ∆
∆ là đường thẳng qua A, vuông góc với d => ∆
⊂
(α) mặt phẳng qua A và vuông góc d
Phương trình mặt phẳng (α): 1(x – 3) – 2(y – 2) + 2(z – 1) = 0 ó x – 2y + 2z – 1 = 0
Khi đó, ![]() khi và chỉ khi ∆ đi qua hình chiếu H của B lên (α)
khi và chỉ khi ∆ đi qua hình chiếu H của B lên (α)
*) Tìm tọa độ điểm H:
Đường thẳng BH đi qua B(2;0;4) và có VTCP là VTPT của (α) có phương trình:

![]()
![]()
=> ![]()
<=> ![]()
∆ đi qua A(3;2;1), H(1;2;2) có VTCP H A → = 2 ; 0 ; - 1 = u → 2 ; b ; c ; u → = 5

Câu 1 : Việc gõ ký hiệu như bạn đề cập ; mình cũng không biết phải làm sao nên cứ dùng xyz vậy thôi.
Ta có:
xyz = 100x +10y +z = 111x -11x +10y +z = 37.3x -(11x-10y-z) chia hết cho 37
=> (11x-10y-z) chia hết cho 37
Lại có:
xyz -yzx = 100x +10y +z -100y -10z -x = 99x -90y -9z = 9.(11x-10y-z) chia hết cho 37
Vậy yzx cũng phải chia hết cho 37
Có thể phát biểu hay hơn là CMR: Khi hoán vị các chữ số của 1 số có 3 chữ số chia hết cho 37 thì được số mới cũng chia hết cho 37.

\(D=\frac{\frac{2}{3}+\frac{2}{7}-\frac{1}{14}}{-\frac{10}{7}+\frac{3}{28}}\)
\(=\frac{\frac{28}{42}+\frac{12}{42}-\frac{3}{42}}{-\frac{40}{28}+\frac{3}{28}}\)
\(=\frac{\frac{37}{42}}{-\frac{37}{28}}\)
\(=\frac{\frac{1}{42}}{-\frac{1}{28}}\) (rút gọn số chia và số bị chia cho 37)
\(=\frac{-28}{42}=-\frac{2}{3}\)
Vậy \(D=-\frac{2}{3}\)

Bài 2:
a) Ta có:
\(S=1-3+3^2-3^3+3^4-3^5+3^6-3^7+...+3^{96}-3^{97}+3^{98}-3^{99}\)
\(=\left(1-3+3^2-3^3\right)+\left(3^4-3^5+3^6-3^7\right)+...+\left(3^{96}-3^{97}+3^{98}-3^{99}\right)\)
\(=1.\left(1-3+3^2-3^3\right)+3^4.\left(1-3+3^2-3^3\right)+...+3^{96}.\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(-20\right)\) \(\text{⋮}\) \(-20\)
Vậy \(S\) \(\text{⋮}\) \(-20\)
Bài 1:
Ta có:
\(A=\left(5m^2-8m^2-9m^2\right).\left(-n^3+4n^3\right)\)
\(=\left[\left(5-8-9\right).m^2\right].\left[\left(-1+4\right).n^3\right]\)
\(=\left(-12\right).m^2.3.n^3\)
\(=\left(m^2.3\right).\left[\left(-12\right)n^3\right]\)
Xét: \(m^2\ge0\) với V m
3>0 nên \(m^2.3\ge0\) với V m
Như vậy để \(A\ge0\) thì \(\left(-12\right)n^3\ge0\)
-12 < 0 nên nếu \(\left(-12\right)n^3\ge0\) thì \(n^3<0\Rightarrow n<0\)
Vậy với n<0 và mọi m thì \(A\ge0\)

Đáp án A
Goi (P) là mặt phẳng đi qua A vuông vởi với giá của u →
⇒ P : 6 x + 1 − 2 y − 2 − 3 z + 3 = 0 ⇔ P : 6 x − 2 y − 3 z = − 1
Gọi B = P ∩ d ⇒ B 4 + 3 t ; 1 + 2 t ; − 2 − 5 t
B ∈ P ⇒ 6. 4 + 3 t − 2 1 + 2 t − 3 − 2 − 5 t = − 1 ⇔ t = − 1 ⇒ B 1 ; − 1 ; 3
Đường thẳng Δ đi qua A − 1 ; 2 ; − 3 và B 1 ; − 1 ; 3 có vtcp u Δ → = A B → = 2 ; − 3 ; 6
⇒ Δ : x − 1 2 = y + 1 − 3 = z − 3 6