Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{3x-y}{x+y}=\frac{3}{4}\)
\(\Leftrightarrow4\left(3x-y\right)=3\left(x+y\right)\)
\(\Leftrightarrow12x-4y=3x+3y\)
\(\Leftrightarrow12x-4y-3x-3y=0\)
\(\Leftrightarrow9x-7y=0\)
\(\Leftrightarrow9x=7y\Leftrightarrow\frac{x}{7}=\frac{y}{9}\)

Ta có: \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\Rightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}\)
Áp dụng tính chất của dãy tỉ số = nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\Rightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}=\left(\frac{a+b}{c+d}\right)^2\left(1\right)\)
\(\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2+b^2}{c^2+d^2}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left(\frac{a+b}{c+d}\right)^2=\frac{a^2+b^2}{c^2+d^2}\left(đpcm\right)\)
đặt a/b = c/d = k (k thuộc N)
=> a = bk
c = dk
thay a và c vào 2 phân số cần so sánh thì = nhau

Phân tích vế trái
= (a+b)^2/(c+d)^2
=a^2+2ab+b^2/(c^2+2cd+d^2)
Mà axd=bxc ( theo đề cho => 2xaxb/2xcxd=1/1=1
=> (a^2+b^2)/(c^2+d^2)
Vậy với a/b=c/d ta có ((a+b)/(c+d))^2= (a^2+b^2)/(c^2+d^2)

(1) Hai đường thẳng vuông góc với nhau là hai đường thẳng cắt nhau tạo thành một góc vuông.
(2) Đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng gọi là đường trung trực của đoạn thẳng ấy.
(3) Hai đường thẳng song song là hai đường thẳng không có điểm chung.
1) 2 đường thẳng vuông góc là 2 đường thẳng cắt nhau và trong các góc tạo thành có 1 góc vuông thì chúng vuông góc với nhau.
2) Đường trung trực của 1 đoạn thẳng là đường thẳng vuông góc với 1 đoạn thẳng tại trung điểm của nó.
3) 2 đường thẳng song song là 2 đường thẳng không có điểm chung.
4) - Định lý là 1 khẳng định suy ra từ những khẳng định được coi là đúng.
- Chứng minh định lý là dùng lập luận để từ giả tiết rút ra kết luận.
5) Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó.![]()

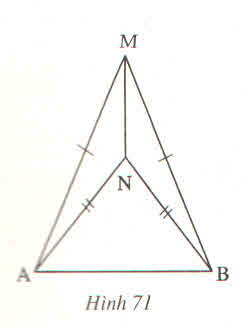
Xét tg AMN và tg BMN có:
MN chung
MA = MB (gt)
NA = NB (gt)
=> tg AMN = tg BMN (c.c.c)
1) Giả thiết: \(\Delta AMN;\Delta BMN\) có: MA = MB và NA = NB.
Kết luận: tg AMN = tg BMN
2) \(\Delta AMN\) và \(\Delta BMN\) có:
MN: cạnh chung
MA = MB (giả thiết)
NA = NB (giả thiết)
Do đó \(\Delta AMN=\Delta BMN\left(c.c.c\right)\)
Suy ra \(\widehat{AMN}=\widehat{BMN}\) (2 góc t/ư).
bạn làm sai chỗ Kết luận: tg AMN = tg BMN VÌ ngta nói chứng minh góc chứ ko phải tg

a/ Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau
b/ GT: Nếu một đường thẳng cắt hai đường thẳng song song
KL: thì hai góc so le trong bằng nhau

Khi chứng minh định lý, ta cần chứng minh định lý đó đúng trong mọi trường hợp có thể xảy ra của giả thiết.
Chọn đáp án C