
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

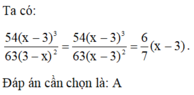

\(ĐKXĐ:\hept{\begin{cases}x\ne\pm2\\x\ne0\end{cases}}\)
a) \(P=\left(\frac{x^2}{x^3-4x}+\frac{6}{6-3x}+\frac{1}{x+2}\right):\left(x-2+\frac{10-x^2}{x+2}\right)\)
\(\Leftrightarrow P=\left(\frac{x^2}{x\left(x-2\right)\left(x+2\right)}-\frac{6}{3\left(x-2\right)}+\frac{1}{x+2}\right):\frac{x^2-4+10-x^2}{x-2}\)
\(\Leftrightarrow P=\frac{x^2-2x\left(x+2\right)+x\left(x-2\right)}{x\left(x-2\right)\left(x+2\right)}:\frac{6}{x-2}\)
\(\Leftrightarrow P=\frac{x^2-2x^2-4x+x^2-2x}{x\left(x-2\right)\left(x+2\right)}\cdot\frac{x-2}{6}\)
\(\Leftrightarrow P=\frac{-6x}{6x\left(x+2\right)}\)
\(\Leftrightarrow P=\frac{-1}{x+2}\)
b) Khi \(\left|x\right|=\frac{3}{4}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{3}{4}\\x=-\frac{3}{4}\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}P=-\frac{1}{\frac{3}{4}+2}=-\frac{4}{11}\\P=-\frac{1}{-\frac{3}{4}+2}=-\frac{4}{5}\end{cases}}\)
c) Để P = 7
\(\Leftrightarrow-\frac{1}{x+2}=7\)
\(\Leftrightarrow7\left(x+2\right)=-1\)
\(\Leftrightarrow7x+14=-1\)
\(\Leftrightarrow7x=-15\)
\(\Leftrightarrow x=-\frac{15}{7}\)
Vậy để \(P=7\Leftrightarrow x=-\frac{15}{7}\)
d) Để \(P\inℤ\)
\(\Leftrightarrow1⋮x+2\)
\(\Leftrightarrow x+2\inƯ\left(1\right)=\left\{\pm1\right\}\)
\(\Leftrightarrow x\in\left\{-3;-1\right\}\)
Vậy để \(P\inℤ\Leftrightarrow x\in\left\{-3;-1\right\}\)

a)(x+y)3-3xy(x+y)
\(=\left(x+y\right)\left(x^2+xy+y^2\right)-3xy\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2+xy+y^2-3xy\right)\)
\(=\left(x+y\right)\left(x^2-2xy+y^2\right)\)
c)\(\left(a+b\right)^2-\left(a-b\right)^2-4ab\)
\(=\left[\left(a+b\right)-\left(a-b\right)\right]\left[\left(a+b\right)+\left(a-b\right)\right]-4ab\)
\(=\left(a+b-a+b\right)\left(a+b+a-b\right)-4ab\)
\(=2b.2a-4ab\)
\(=4ab-4ab=0\)

\(\frac{x^7+x^6+x^5+x^4+x^3+x^2+x+1}{x^2-1}\left(DK:x\ne-1;x\ne1\right)\)
\(=\frac{x^4\left(x^3+x^2+x+1\right)+\left(x^3+x^2+x+1\right)}{x^2-1}\)
\(=\frac{x^4\left[x\left(x^2+1\right)+x^2+1\right]+\left[x\left(x^2+1\right)+x^2+1\right]}{x^2-1}\)
\(=\frac{\left(x^4+1\right)\left(x+1\right)\left(x^2+1\right)}{\left(x-1\right)\left(x+1\right)}=\frac{\left(x^2+1\right)\left(x^4+1\right)}{x-1}\)
\(\frac{x^7+x^6+x^5+x^4+x^3+x^2+x+1}{x^2-1}\)
\(=\frac{x^6\left(x+1\right)+x^4\left(x+1\right)+x^2\left(x+1\right)+\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(=\frac{\left(x+1\right)\left(x^6+x^4+x^2\right)}{\left(x+1\right)\left(x-1\right)}\)
\(=\frac{x^6+x^4+x^2}{x+1}\)
\(=\frac{x^2\left(x^3+x^2+1\right)}{x+1}\)

\(1,\frac{x^6+2x^3y^3+y^6}{x^7-xy^6}=\frac{\left(x^3+y^3\right)^2}{x\left(x^6-y^6\right)}=\frac{\left(x^3+y^3\right)^2}{x\left(x^3-y^3\right)\left(x^3+y^3\right)}=\frac{x^3+y^3}{x\left(x^3-y^3\right)}\)
\(2,=\frac{\left(a+b\right)^2-c^2}{\left(a+c\right)^2-b^2}=\frac{\left(a+b+c\right)\left(a+b-c\right)}{\left(a+b+c\right)\left(a+c-b\right)}=\frac{a+b-c}{a+c-b}\)
pt thành nhân tử là ra

tôi cũng cung thiên yết nè nhưng lại là cậu bé mà thiên yết hợp với cung gì nhất vậy add friend nha