Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: A
HD Giải:
Áp dụng quy tắc nắm bàn tay phải ta có chiều ![]() như hình vẽ.
như hình vẽ.
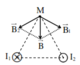
Do ![]() hợp với nhau 1 góc 1200 nên:
hợp với nhau 1 góc 1200 nên:
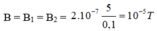

a)Hai dây dẫn cùng chiều.
\(B_1=2\cdot10^{-7}\cdot\dfrac{I_1}{r_1}=2\cdot10^{-7}\cdot\dfrac{5}{0,05}=2\cdot10^{-5}T\)
\(B_2=2\cdot10^{-7}\cdot\dfrac{I_2}{r_2}=2\cdot10^{-7}\cdot\dfrac{1}{0,05}=4\cdot10^{-6}T\)
\(B=B_1+B_2=2\cdot10^{-5}+4\cdot10^{-6}=2,4\cdot10^{-5}T\)
b)Hai dây dẫn ngược chiều nhau.
\(B_1=2\cdot10^{-7}\cdot\dfrac{I_1}{r_1}=2\cdot10^{-7}\cdot\dfrac{5}{0,05}=2\cdot10^{-5}T\)
\(B_2=2\cdot10^{-7}\cdot\dfrac{I_2}{r_2}=2\cdot10^{-7}\cdot\dfrac{1}{0,15}=1,33\cdot10^{-6}T\)
\(B=\left|B_1-B_2\right|=\left|2\cdot10^{-5}-1,33\cdot10^{-6}\right|=1,867\cdot10^{-5}T\)
c)Hai dây dẫn vuông góc nhau (vì \(\sqrt{6^2+8^2}=10\))
\(B_1=2\cdot10^{-7}\cdot\dfrac{I_1}{r_1}=2\cdot10^{-7}\cdot\dfrac{5}{0,06}=1,67\cdot10^{-5}T\)
\(B_2=2\cdot10^{-7}\cdot\dfrac{I_2}{r_2}=2\cdot10^{-7}\cdot\dfrac{1}{0,08}=2,5\cdot10^{-6}T\)
\(B=\sqrt{B_1^2+B_2^2}=\sqrt{\left(1,67\cdot10^{-5}\right)^2+\left(2,5\cdot10^{-6}\right)^2}=1,688\cdot10^{-5}T\)

\(MA+MB=AB\) Nên M có vti như hình
Xác định chiều cảm ứng từ do I1 và I2 gây ra tại M bằng quy tắc nắm bàn tay phải được như hình vẽ
\(B\overrightarrow{M}=B\overrightarrow{A}+B\overrightarrow{B}\)
\(\rightarrow B_M=B_A+B_B=2.10^{-2}\left(\frac{I1}{MA}+\frac{I2}{MB}\right)\)
\(=2.10^{-7}.\left(\frac{2}{0,06}+\frac{4}{0,04}\right)=2,67.10^{-5}\left(T\right)\)
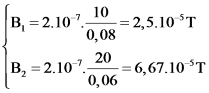 + Thay số ta được
+ Thay số ta được
Giả sử : I1 ; I2 Chay trong 2 dây dẫn , vuông góc với mặt phẳng hình vẽ . Từ trường \(\overline{B}_1\)do dòng I1 gây ra , hợp với từ trường \(\overline{B}_2\)
do dòng I2 gây ra góc \(a=120^o\).
\(B_1=B_2=10^{-5}T\Rightarrow B_M=B_1=B_2=10^{-5}T\)