Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nối C với D. Ta thấy CBD hay CDA = 1/2 ABC = ABC : 2 = 90 : 2 = 45 ( cm2 )
Ta thấy AKD, KED, ECD có chung đường cao và đều có đáy = 1/3 đáy AC. Vậy suy ra các hình AKD, KED, ECD = 1/3 CDA = 45 : 3
= 15 ( cm2 )
AED = 2/3 CDA = 45 x 2/3 = 30 ( cm2 ) hoặc AED = ADK + EKD = 15 + 15 = 30 ( cm2 )
Đáp số : 30 cm2

Bài này nói thật thì mình học ở lớp rồi .Nhưng nà bạn phải ghi hết đầu bài thì mọi người mới hiểu đc là đề bài như thế nào chứ.Nếu ko thì sao mà giải cho bạn đc?Mk mong câu hỏi của bạn đấy.Nhớ vẽ hình vào nhé bạn

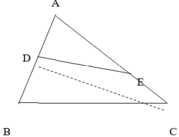
Nối DC ta có
- SCAD = 1/2 SCAB (vì cùng chiều cao hạ từ C xuống AB và đáy DB = DA = 90 : 2 = 45 cm2)
- SDAE = 2/3 SADC (Vì cùng chiều cao hạ từ D xuống AC và đáy
E = 2/3 AC) = 45 × 2 3 = 30 (cm2)
Đáp số SAED = 30 c m 2

Nối C với D.Ta thấy CBD hay CDA =1/2 ABC=ABC:2=90:2=45(cm vuông)
Ta thấy AKD,KED,ECD có chung đường cao và đều có đáy =1/3 đáy AC. Vậy suy ra các hình AKD,KED,ECD=1/3CDA=45:3=15(cm vuông)
AED=2/3 CDA=45x2/3=30 (cm vuông) hoặc AED=ADK+EKD=15+15=30(cm vuông)
Đ/S:30 cm vuông

S ADC = 1/2 S ABC và bằng : 90 : 2 = 45 <cm2>
S ADE = 2/3 S ADC và bằng : 45 x 2/3 = 30 <cm2>

Ta có : \(S_{ACD}=S_{BCD}\) ( vì chung đường cao hạ từ đỉnh C xuống đáy AB và đáy AD = đáy BD )
Diện tích tam giác ACD là :
\(90\div2=45\) ( cm² )
\(S_{AED}=\frac{2}{3}S_{ACD}\) ( vì chung đường cao hạ từ đỉnh D xuống đáy AC và đáy AE = \(\frac{2}{3}\) đáy AC)
Diện tích tam giác AED là :
\(45\times\frac{2}{3}=30\) ( cm ²)
Đáp số : 30 cm²