Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A = \(\dfrac{4\sqrt{x}+9}{2\sqrt{x}+1}\)
Mà \(4\sqrt{x}+9>0\)
\(2\sqrt{x}+1>0\)
=> A > 0
A = \(\dfrac{2\left(2\sqrt{x}+1\right)+7}{2\sqrt{x}+1}\) = \(2+\dfrac{7}{2\sqrt{x}+1}\)
Mà \(2\sqrt{x}+1\ge1< =>\dfrac{7}{2\sqrt{x}+1}\le7\)
<=> \(A\le9\)
<=> 0 < A \(\le9\)
Mà A thuộc Z
<=> A \(\in\){1;2;3;4;5;6;7;8;9}
Đến đây bn thay A vào để tìm x nhé
A = \(\dfrac{2\left(2\sqrt{x}+1\right)+7}{2\sqrt{x}+1}=2+\dfrac{7}{2\sqrt{x}+1}\)
Mà \(2\sqrt{x}+1>0< =>\dfrac{7}{2\sqrt{x}+1}>0\)
<=> A > 2
Có \(2\sqrt{x}+1\ge1< =>\dfrac{7}{2\sqrt{x}+1}\le7\)
<=> \(A\le9\)
<=> 2 < A \(\le9\)
Mà A thuộc Z
<=> \(A\in\left\{3;4;5;6;7;8;9\right\}\)
Đến đây bn thay A vào để tìm x nhé

A = \(\dfrac{6\sqrt{x}+8}{3\sqrt{x}+2}=2+\dfrac{4}{3\sqrt{x}+2}\)
Có \(3\sqrt{x}+2>0< =>\dfrac{4}{3\sqrt{x}+2}>0\) <=> A > 2
Có: \(3\sqrt{x}+2\ge2< =>\dfrac{4}{3\sqrt{x}+2}\le2\) <=> A \(\le4\)
<=> 2 < A \(\le4\)
Mà A nguyên
<=> \(\left[{}\begin{matrix}A=3\\A=4\end{matrix}\right.\)
TH1: A = 3
<=> \(\dfrac{4}{3\sqrt{x}+2}=1\)
<=> \(3\sqrt{x}+2=4< =>x=\dfrac{4}{9}\)
TH2: A = 4
<=> \(\dfrac{4}{3\sqrt{x}+2}=2< =>3\sqrt{x}+2=2< =>x=0\)

\(A=\dfrac{\cos^217^o+2\cos^273^o}{\cot65^o\cot25^o}-\sin^217^o\)
\(A=\dfrac{\left(\cos^217^o+\cos^273^o\right)+\cos^273^o}{\tan25^o\cot25^o}-\sin^217^o\)
(áp dụng công thức \(\cot\alpha=\tan\left(90^o-\alpha\right)\))
\(A=\left(\cos^217^o+\sin^217^o\right)+\sin^217^o-\sin^217^o\)
(áp dụng công thức \(\tan\alpha.\cot\alpha=1\) và \(\cos\alpha=\sin\left(90^o-\alpha\right)\))
\(A=1\)

Bạn tham khảo nha !Sorry vì mất thời gian :))
https://thi.tuyensinh247.com/de-khao-sat-chat-luong-thang-9-mon-toan-lop-9-nam-2019-thpt-ta-quang-buu-c30a48031.html
Bạn tham khảo nha !
https://toanmath.com/2019/05/de-thi-thu-thpt-quoc-gia-mon-toan-nam-2019-so-gddt-nam-dinh.html
Chúc bạn học tốt !

Xét A = \(\sqrt{x}-3+\dfrac{36}{\sqrt{x}-3}+3\)
Áp dụng BDT Co-si, ta có:
\(\left(\sqrt{x}-3\right)+\dfrac{36}{\sqrt{x}-3}\ge2\sqrt{\left(\sqrt{x}-3\right).\dfrac{36}{\sqrt{x}-3}}\) = 12
=> A \(\ge15\)
Dấu "=" xảy ra <=> x = 81

`5)A=sqrtx+36/(sqrtx-3)`
`A=sqrtx-3+36/(sqrtx-3)+3`
ÁP dụng bđt cosi ta có:
`sqrtx-3+36/(sqrtx-3)>=2sqrt{36}=12`
`=>A>=12+3=15`
Dấu "=" xảy ra khi `sqrtx-3=36/(sqrtx-3)`
`<=>(sqrtx-3)^2=36`
`<=>sqrtx-3=6`
`<=>sqrtx=9`
`<=>x=81`
Không có Max.
\(A=\sqrt{x}-3+\dfrac{36}{\sqrt{x}-3}+3\)
Theo BĐT Cô Si ta có:
\(\sqrt{x}-3+\dfrac{36}{\sqrt{x}-3}\ge2\sqrt{\sqrt{x}-3.\dfrac{36}{\sqrt{x}-3}}\)
⇔\(\sqrt{x}-3+\dfrac{36}{\sqrt{x}-3}\ge12\)
⇔\(A\ge12+3\)
⇔\(A\ge15\)
⇒\(Min_A=15\)
Dấu = xảy ra khi và chỉ khi : \(\sqrt{x}-3=\dfrac{36}{\sqrt{x}-3}\)
⇔\(\left(\sqrt{x}-3\right)^2=36\)
⇔\(\sqrt{x}-3=6\)
⇔\(\sqrt{x}=9\)
⇔\(x=81\)

Lời giải:
Theo đề ta có:
\(\text{sđc(AD)}=\frac{1}{3}\text{sđc(AB)}=\frac{1}{9}[\text{sđc(AB)+sđc(BC)+sđc(CD)}]\)
\(=\frac{1}{9}(360^0-\text{sđc(AD)})\)
\(\Rightarrow \text{sđc(AD)}=36^0\)
\(\widehat{BEC}=\frac{\text{sđc(BC)-sđc(AD)}}{2}=\frac{3\text{sđc(AD)}-\text{sđc(AD)}}{2}=\text{sđc(AD)}=36^0\)

\(2,ĐK:\left\{{}\begin{matrix}\dfrac{2}{a+5}\ge0\\a+5\ne0\end{matrix}\right.\Leftrightarrow a+5>0\Leftrightarrow a>-5\left(C\right)\\ 3,M=2\sqrt{3}=\sqrt{12}< \sqrt{15}=N\left(C\right)\\ 4,=\left|3-\sqrt{3}\right|=3-\sqrt{3}\left(A\right)\\ 5,=\dfrac{3\sqrt{5}-3\sqrt{3}+3\sqrt{5}+3\sqrt{3}}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}=\dfrac{6\sqrt{5}}{2}=3\sqrt{5}\left(C\right)\)


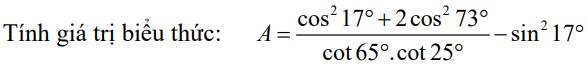


ĐKXĐ: \(x\geq -5\).
\(PT\Leftrightarrow\left(x-\dfrac{3}{2}\right)^2=\left(\sqrt{x+5}+\dfrac{1}{2}\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{3}{2}=\sqrt{x+5}+\dfrac{1}{2}\left(1\right)\\\dfrac{3}{2}-x=\sqrt{x+5}+\dfrac{1}{2}\left(2\right)\end{matrix}\right.\).
+) \(\left(1\right)\Leftrightarrow x-2=\sqrt{x+5}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge2\\x^2-4x+4=x+5\end{matrix}\right.\Leftrightarrow x=\dfrac{5+\sqrt{29}}{2}\).
+) \(\left(2\right)\Leftrightarrow\sqrt{x+5}=1-x\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le1\\x+5=x^2-2x+1\end{matrix}\right.\Leftrightarrow x=-1\).
Do đó hai nghiệm của pt này có tổng bằng \(\dfrac{3+\sqrt{29}}{2}\). Chọn A
+)