Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Định hướng tư duy giải
Ta có:

Ta dồn X về
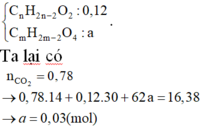
Để thuận tiện cho việc biện luận các chất trong X.
Ta dồn X về
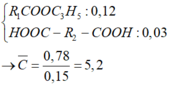
→ ∑ m R 1 , R 2 = 16 , 38 - 0 , 12 . 85 - 0 , 03 . 90 = 3 , 48 gam
→ BTNT . C n C t r o n g R 1 + n C t r o n g R 2 = 0 , 78 - 0 , 12 . 4 - 0 , 03 . 2 = 0 , 24
+ Nếu số C trong R2 là 0 thì C R 1 = 0 , 24 0 , 12 = 2 loại .
+ Nếu số C trong R2 là 1 thì C R 1 = 0 , 24 - 0 , 03 0 , 12 = 1 , 75
+ Nếu số C trong R2 là 2 thì C R 1 = 0 , 24 - 0 , 03 . 2 0 , 12 = 1 , 5
+ Nếu số C trong R2 là 3 thì C R 1 = 0 , 24 - 0 , 03 . 3 0 , 12 = 1 , 25
+ Nếu số C trong R2 là 4 thì C R 1 = 0 , 24 - 0 , 03 . 4 0 , 12 = 1 loại .
Dễ thấy với các trường hợp của axit thì este luôn là este của CH3COOH và C2H5COOH.

Định hướng tư duy
Ta có:
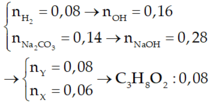
Dồn chất cho m gam E
→ COO : 0 , 22 C : 1 , 04 H 2 : 0 , 72
→ x ế p h ì n h π + C C 2 H 3 C O O - C 3 H 6 - O O C C 2 H 3 : 0 , 08 C 2 H 3 C O O C 6 H 5 : 0 , 06
→ C 2 H 3 C O O - C 3 H 6 - O O C C 2 H 3 : 0 , 08 → 62 , 37 % .

Chọn đáp án B
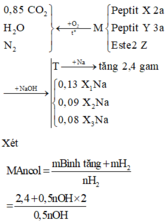
thử nOH lần lượt với 0,13; 0,09 và 0,08
Thấy chỉ khi nOH = 0,08 thì Mancol = 62 là hợp lý Þ T là C2H4(OH)2 (0,04 mol)
BTNT.C
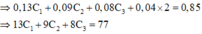
Chỉ có
![]()
là phù hợp
Gọi số mắt xích trong X và Y
lần lượt là x, y và z là số liên kết p
trong gốc hiđrocacbon của X3

Vậy X là pentapeptit (0,02 mol), Y là tetrapeptit (0,03 mol) và X3 là C2H3COOH




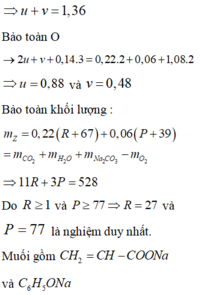
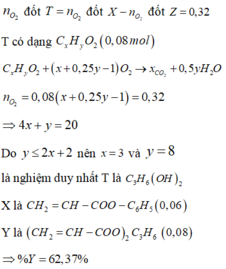
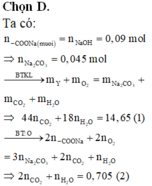

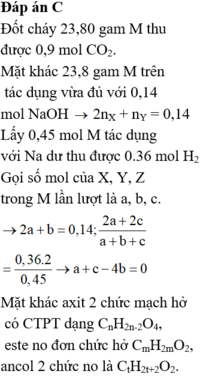

Đáp án A
Định hướng tư duy giải
Ta có: