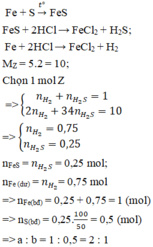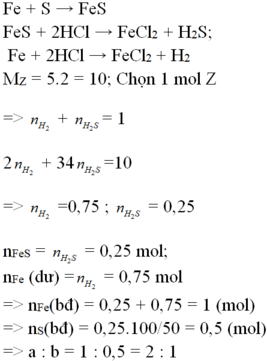Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
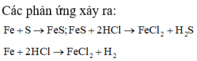
Hỗn hợp khí Z gồm H2S và H2. Đặt nFe=1mol . Dựa vào phương trình phản ứng ta thấy vì số mol khí sinh ra luôn là 1 mol với bất kì hiệu suất và tỉ lệ a:b nào nên:
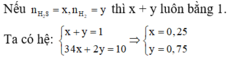
Theo đề bài hiệu suất phản ứng là 50% nhưng do chưa biết Fe hay S dư nên phải xét hai trường hợp. Tuy nhiên khi nhìn vào đáp án có thể thấy số mol sắt lớn hơn số mol lưu huỳnh nên hiệu suất được tính theo lưu huỳnh. Bảo toàn lưu huỳnh suy ra
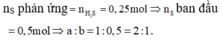

Đáp án A
Các phản ứng xảy ra:
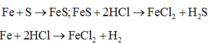
Hỗn hợp khí Z gồm H2S và H2. Đặt nFe=1mol . Dựa vào phương trình phản ứng ta thấy vì số mol khí sinh ra luôn là 1 mol với bất kì hiệu suất và tỉ lệ a:b nào nên:
Nếu ![]() thì x + y luôn bằng 1. Ta có hệ:
thì x + y luôn bằng 1. Ta có hệ:
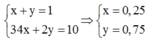
Theo đề bài hiệu suất phản ứng là 50% nhưng do chưa biết Fe hay S dư nên phải xét hai trường hợp. Tuy nhiên khi nhìn vào đáp án có thể thấy số mol sắt lớn hơn số mol lưu huỳnh nên hiệu suất được tính theo lưu huỳnh. Bảo toàn lưu huỳnh suy ra
nS phản ứng
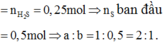

Đáp án D
Chọn 1 mol hỗn hợp X ban đầu thì
![]()
Theo quy tắc đường chéo hoặc giải hệ ta dễ dàng xác định được trong X có
![]()
Xét cân bằng ![]()
Mol ban đầu 0,75 0,25
Mol phản ứng 2x x 2x
Mol cân bằng (0,75 – 2x) (0,25 – x) 2x
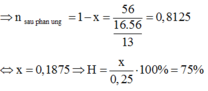

A + H2SO4 → Hỗn hợp khí ⇒ Fe dư; khí Y gồm: H2 ( x mol) và H2S (y mol)
⇒ x + y = 0,1 mol (1)
Bảo toàn S: nH2S = nFeS = nS = y mol
nFe dư = nH2 = x
Bảo toàn Fe: nFe = nFeS + nFe dư = x + y
mX = 56(x + y ) + 32y = 7,2g (2)
Từ (1)(2) ⇒ x = 0,05 mol; y = 0,05 mol
MY = mY : nY = (0,05.2 + 0,05.34) : 0,1 = 18 ⇒ dY/H2 = 9
Gọi \(\left\{{}\begin{matrix}n_{Fe}=a\left(mol\right)\\n_{FeS}=b\left(mol\right)\end{matrix}\right.\left(đk:a,b>0\right)\)
TH1: S dư
Vậy toàn bộ lượng khí sinh ra là H2S
\(d_{Y\text{/}H_2}=d_{H_2S\text{/}H_2}=\dfrac{34}{2}=17\)
TH2: Fe dư
\(n_{khí}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\)
Bảo toàn KL: \(m_A=m_X=7,2\left(g\right)\)
PTHH:
\(Fe+2HCl\rightarrow FeCl_2+H_2\uparrow\)
a----------------------------->a
\(FeS+2HCl\rightarrow FeCl_2+H_2S\uparrow\)
b-------------------------------->b
Ta có hệ phương trình: \(\left\{{}\begin{matrix}56a+88b=7,2\\a+b=0,1\end{matrix}\right.\)
\(\Leftrightarrow a=b=0,05\left(TM\right)\)
\(M_Y=\dfrac{0,05.\left(2+34\right)}{0,1}=18\left(g\text{/}mol\right)\\ \rightarrow d_{Y\text{/}H_2}=\dfrac{18}{2}=9\)