Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Phương pháp
Nhẩm nghiệm của phương trình hoành độ giao điểm, từ đó tìm điều kiện để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.

Để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt thì phương trình x 2 + ( m + 3 ) x + m 2 = 0 phải có hai nghiệm phân biệt khác 1
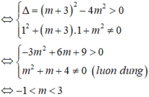
Do đó với -1<m<3 thì đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt
![]()

(Cm) tiếp xúc với trục hoành khi và chỉ khi hệ sau có nghiệm
x 3 - 2 m x 2 + m 2 x + 1 - m = 0 3 x 2 - 4 m x + m 2 = 0 ⇒ x 3 - 2 m x 2 + m 2 x + 1 - m = 0 x = m ; x = m 3 ⇒ m ∈ - 3 ; 1 ; 3 2
Do m ∈ Z nên m = -3; m = 1
Vậy có 2 giá trị nguyên của m thỏa mãn yêu cầu bài toán
Đáp án C

Đáp án B.
Số giao điểm là số nghiệm của phương trình x 3 − 3 x 2 − 9 x + m = 0
⇔ m = − x 3 + 3 x 2 + 9 x
Xét
f x = − x 3 + 3 x 2 + 9 x ⇒ f ' x = − 3 x 2 + 6 x + 9
f ' x = 0 ⇔ x = − 1 x = 3
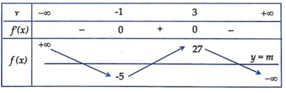
Từ bảng biến thiên ⇒ − 5 < m < 27 thỏa mãn yêu cầu đề bài toán.
=>Có 31 giá trị m thỏa mãn.

Đáp án B
Ta có
y ' = 6 x 2 − 6 m + 3 x + 18 m , ⇒ y ' = 0 ⇔ x = 3 x = m
để đường thẳng Ox là tiếp tuyến thì cực trị của hàm số nằm trên Ox
⇔ y 3 = 0 y m = 0 ⇔ 9 m − 36 = 0 m 3 − 9 m 2 + 8 = 0 ⇔ m = 4 m − 1 m 2 − 8 m − 8 = 0
Từ đây ta chọn đáp án B với m=4

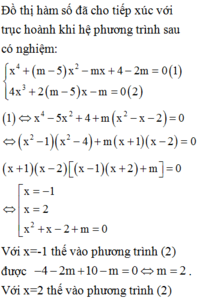





Chọn B.
Đồ thị hàm số đã cho tiếp xúc với trục hoành khi và chỉ khi hệ phương trình sau có nghiệm
Vậy ta chỉ có một giá trị nguyên của tham số m thỏa mãn điều kiện đề bài là m=1