Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : MB+NB=AB=MB+AM
Suy ra : NB=AM
Tương tự : BM=NC
Ta có: \(\widehat{A}=60o\)
Suy ra: \(\widehat{D}=180o-\widehat{A}=120o\)
Dễ thấy, tam giác BMD=tam giác CND (c.g.c)
\(=>\left\{{}\begin{matrix}MD=ND\left(1\right)\\\widehat{BDM}=\widehat{CDN}\end{matrix}\right.\)
Ta có: \(\widehat{BDN}+\widehat{CDN}=60o=>\widehat{BDN}+\widehat{BDM}=60o\)
Hay \(\widehat{MDN}=60o\left(2\right)\)
Từ (1) và (2) => Tam giác MDN là tam giác đều
Chứ o ở sau các số là độ nha bn, mk ko bik cách gõ nên gõ tạm chữ o.
Chúc bn học tốt!

1) hình tự vẽ nhé
a) Vì ABCD là hình thoi (gt)
\(\Rightarrow AB=BC\left(đn\right)\)
\(\Rightarrow\Delta ABC\)cân tại B
Mà \(\widehat{B}=60^0\)
\(\Rightarrow\Delta ABC\)là tam giác đều
b) Vì \(\Delta ABC\)đều(cmt)\(\Rightarrow AB=BC=AC=a\)
Gọi O là giao điểm 2 đường chéo BD và AC
Vì ABCD là hình thoi (gt) \(\Rightarrow DB\perp AC\left(tc\right)\)
\(\Rightarrow BO\perp AC\)
Vì tam giác ABC đều mà trong tam giác ABC thì BO là đường cao ứng với cạnh AC
\(\Rightarrow BO\)là đường trung tuyến ứng vs cạnh AC(tc)
\(\Rightarrow O\)là trung điểm của AC
\(\Rightarrow AO=OC=\frac{1}{2}AC=\frac{1}{2}a\)
Áp dụng định lý Py-ta-go vào tam giác BOC vuông tại O ta được:
\(BO^2+OC^2=BC^2\)
\(BO^2+\frac{1}{4}a^2=a^2\)
\(BO^2=\frac{3}{4}a^2\)
\(\Rightarrow BO=\frac{\sqrt{3}}{2}a\)
Ta có: \(S_{ABC}=\frac{1}{2}BO.AC=\frac{1}{2}.\frac{\sqrt{3}a}{2}.a\)
\(=\frac{\sqrt{3}}{4}a^2\)
CMTT \(S_{ADC}=\frac{\sqrt{3}}{4}a^2\)
\(S_{ABCD}=S_{ADC}+S_{ABC}=\frac{\sqrt{3}}{2}a^2\)

a: Xét ΔBAM và ΔBCN có
BA=BC
góc BAM=góc BCN
AM=CN
Do đó: ΔBAM=ΔBCN
=>BM=BN
=>ΔBMN cân tại B
b: DM+MA=DA
DN+NC=DC
mà DA=DC và MA=NC
nên DM=DN
BM=BN
DM=DN
Do đó: BD là trung trực của MN
=>BD vuông góc MN
c: Xét ΔABD có AB=AD và góc A=60 độ
nên ΔABD đều
ΔABD đều có BM là trung tuyến
nên BM là phân giác của góc ABD(1)
Xét ΔCBD có CB=CD và góc C=60 độ
nên ΔCBD đều
ΔCBD đều có BN là trung tuyến
nên BN là phân giác của góc DBC(2)
Từ (1), (2) suy ra góc MBN=1/2(góc ABD+góc CBD)
=1/2*góc ABC
=60 độ
Xét ΔBMN có BM=BN và góc MBN=60 độ
nên ΔBMN đều
=>góc BMN=60 độ
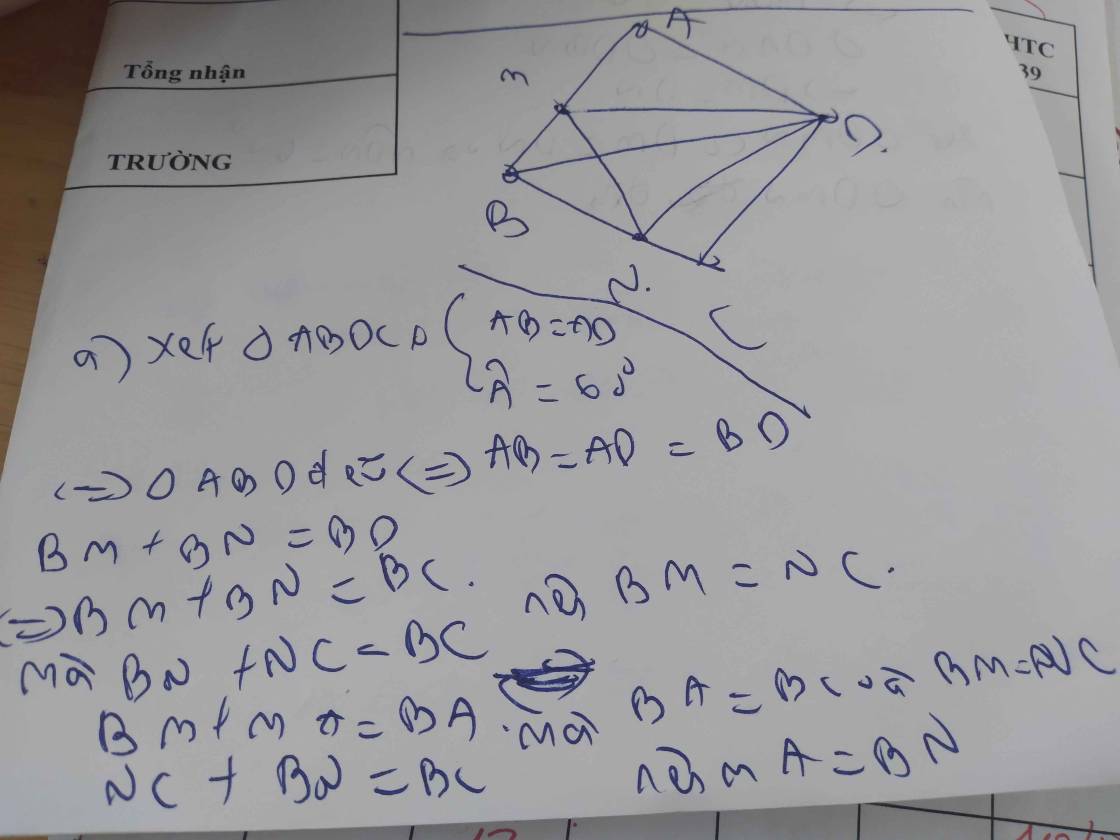


Hình tự vẽ nhé
Ta có:
MB + NB = AB = MB + AM
=> AM = NB
<=> BM = NC (gt)
Theo đề ra: \(\widehat{A}=60^o\)
=> \(\widehat{D}=\widehat{B}=120^o\)
Dễ thấy \(\Delta BMD=\Delta CND\)(c-g-c)
\(\Rightarrow\hept{\begin{cases}MD=ND\\\widehat{BDM}=\widehat{CDN}=60^o\end{cases}}\)
Ta có:
\(\widehat{BDN}+\widehat{CDN}=60^o\)
\(\Rightarrow\widehat{BDN}+\widehat{BDM}=60^o\)hay \(\widehat{MDN}=60^o\)
Từ \(MD=ND\)và \(\widehat{MDN}=60^o\)=> Tam giác MDN là tam giác đều