K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
mọi ng hộ e câu 6 vs câu 9 vs ạ
2
23 tháng 7 2021
c) Ta có: \(\dfrac{1}{\sqrt{3}+\sqrt{2}}+\dfrac{\sqrt{6}}{\sqrt{3}}-3\cdot\sqrt{\dfrac{1}{3}}\)
\(=\sqrt{3}-\sqrt{2}+\sqrt{2}-\sqrt{3}\)
=0
10 tháng 9 2023
6: ĐKXĐ: y<>0; y<>2; y<>-2; y<>3
a: \(P=\left(\dfrac{-\left(y+2\right)}{y-2}-\dfrac{4y^2}{\left(y-2\right)\left(y+2\right)}+\dfrac{y-2}{y+2}\right):\dfrac{y\left(y-3\right)}{y^2\left(2-y\right)}:\dfrac{1}{y-3}\)
\(=\dfrac{-y^2-4y-4-4y^2+y^2-4y+4}{\left(y-2\right)\left(y+2\right)}\cdot\dfrac{y\left(2-y\right)}{y-3}\cdot\dfrac{y-3}{1}\)
\(=\dfrac{-4y^2-8y}{\left(y-2\right)\left(y+2\right)}\cdot\dfrac{-y\left(y-2\right)}{1}\)
\(=4y^2\)
b: 2y^2-3y-2=0
=>2y^2-4y+y-2=0
=>(y-2)*(2y+1)=0
=>y=2(loại) hoặc y=-1/2(nhận)
Khi y=-1/2 thì P=4*(-1/2)^2=1
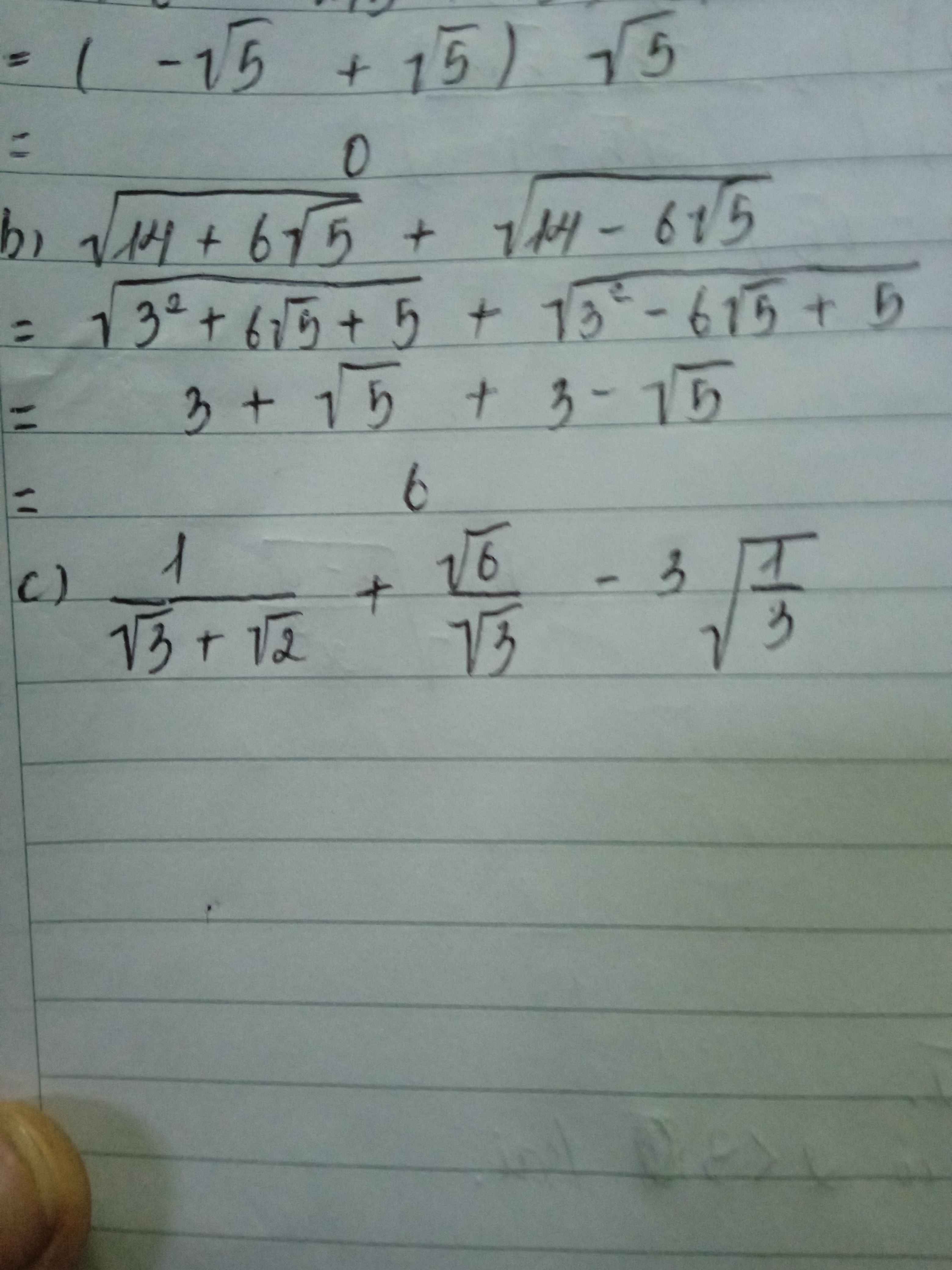
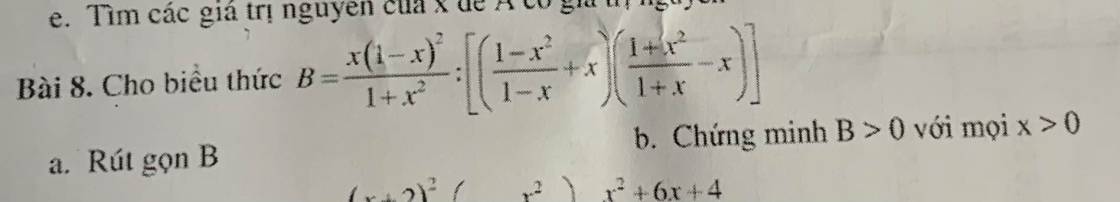
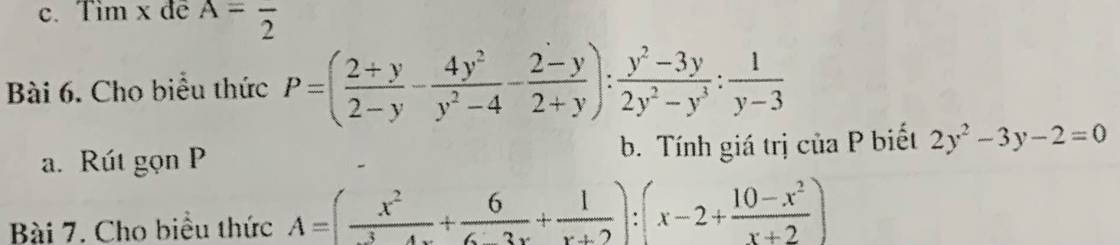
8:
ĐKXĐ: x<>1; x<>-1; x<>-1/2
a:
\(B=\dfrac{x\left(x-1\right)^2}{x^2+1}:\left[\left(\dfrac{\left(1-x\right)\left(1+x\right)}{\left(1-x\right)}+x\right)\cdot\dfrac{1+x^2-x-x^2}{1+x}\right]\)
\(=\dfrac{x\left(x-1\right)^2}{x^2+1}:\left[\left(1+x+x\right)\cdot\dfrac{1-x}{1+x}\right]\)
\(=\dfrac{x\left(x-1\right)^2\left(x+1\right)}{\left(x^2+1\right)\left(2x+1\right)\left(x-1\right)}\)
\(=\dfrac{x\left(x-1\right)\left(x+1\right)}{\left(x^2+1\right)\left(2x+1\right)}\)
b: Khi x>0 thì x-1 chưa chắc lớn hơn 0
Do đó: B chưa chắc lớn hơn 0 khi x>0 đâu nha bạn