Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

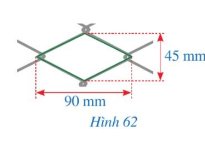
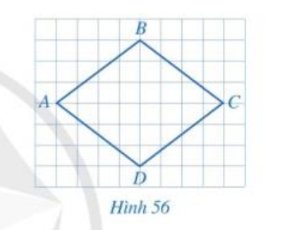
Giả sử mắt lưới cần tính độ dài cạnh là hình thoi ABCD.
Có. AC = 45mm; BD = 90mm.
Gọi O là giao điểm của AC và BD.
Vì ABCD là hình thoi nên
\(\begin{array}{l}OA = OC = \dfrac{{AC}}{2} = \dfrac{{45}}{2} = 22,5(mm)\\OB = OD = \dfrac{{BD}}{2} = \dfrac{{90}}{2} = 45(mm)\end{array}\)
Xét \(\Delta AOB\) vuông tại O có:
\(\begin{array}{l}A{O^2} + O{B^2} = A{B^2}\\{(22,5)^2} + {(45)^2} = A{B^2} \Rightarrow A{B^2} = 2.531,25 \Rightarrow AB \approx 50(mm)\end{array}\)

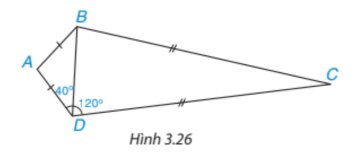
* Xét tam giác ABD cân tại A (vì AB = AD) ta có:
• \(\widehat {AB{\rm{D}}} = \widehat {A{\rm{D}}B} = {40^o}\)
• \(\widehat A + \widehat {AB{\rm{D}}} + \widehat {A{\rm{D}}B} = {180^o}\)
Suy ra \(\widehat A\)=180°−\(\widehat {AB{\rm{D}}}\)−\(\widehat {A{\rm{D}}B}\)=180°−40°−40°=100°
Ta có \(\widehat {A{\rm{D}}B} + \widehat {B{\rm{D}}C}\)=120° suy ra \(\widehat {B{\rm{D}}C}\)=120°−\(\widehat {A{\rm{D}}B}\)=120°−40°=80°.
* Xét tam giác BCD cân tại C (vì BC = CD) ta có:
• \(\widehat {CB{\rm{D}}} = \widehat {C{\rm{D}}B}\)=80°
• \(\widehat C + \widehat {CB{\rm{D}}} + \widehat {C{\rm{D}}B}\)=180°
Suy ra \(\widehat C\)=180°−\(\widehat {CB{\rm{D}}} - \widehat {C{\rm{D}}B}\)=180°−80°−80°=20°
Ta có: \(\widehat {ABC} = \widehat {AB{\rm{D}}} + \widehat {CB{\rm{D}}}\)=40°+80°=120o
Vậy số đo các góc của tứ giác ABCD là \(\widehat A = {100^o};\widehat {ABC} = {120^o};\widehat C = {20^o}\)

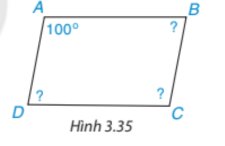
Vì ABCD là hình bình hành nên: \(\widehat A = \widehat C;\widehat B = \widehat D\) ta có:
\(\begin{array}{l}\widehat A = \widehat C = {100^o}\\\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\\{100^o} + \widehat B + {100^o} + \widehat B = {360^o}\\2\widehat B + {200^o} = {360^o}\end{array}\)
Suy ra: \(2\widehat B = {360^o} - {200^o} = {160^o}\)
Do đó: \(\widehat B = {80^o}\) suy ra: \(\widehat B = \widehat D = {80^o}\)
Vậy các góc của hình bình hành ABCD là: \(\widehat A = {100^o};\widehat C = {100^o};\widehat B = {80^o};\widehat D = {80^o}\)

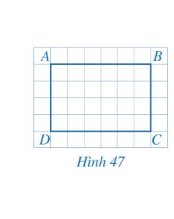
Tứ giác ABCD có: \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\)

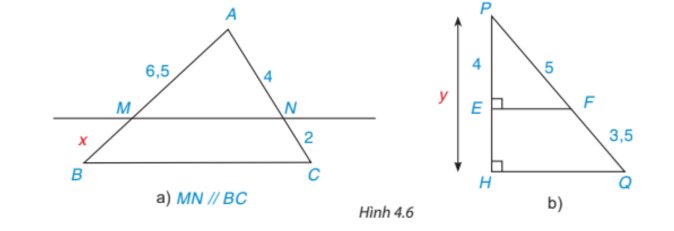
a)
Xét tam giác ABC có MN//BC
`=>(AM)/MB=(AN)/(NC)` (định lí thales)
`=>(6,5)/x=4/2`
`=>x=3,25`
b)
có QH⊥PH (hình vẽ)
FE⊥PH (hình vẽ)
Suy ra EF//HQ (từ vuông góc đến song song)
Xét tam giác PHQ có EF//HQ (cmt)
`=>(PE)/(PH)=(PF)/(PQ)` (định lí thales)
`=>4/x=5/(5+3,5)`
`=>4/x=5/(8,5)`
`=>x=6,8`

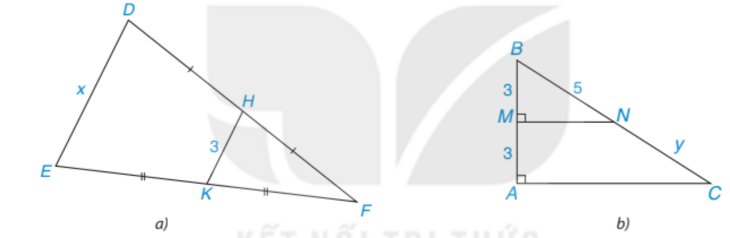
a. Do H, K lần lượt là trung điểm cạnh DF, EF
⇒ HK là đường trung bình của tam giác DEF.
⇒ DE = 2 HK = 2 \(\times\) 3 = 6.
b. Do M là trung điểm cạnh AB mà MN // AC (cùng vuông góc với AB)
⇒ MN là đường trung bình của tam giác ABC.
⇒ N là trung điểm của cạnh BC
⇒ y = NB = NC = 5.

Các cặp cạnh đối song song
=>Tứ giác đó là hình bình hành
=> Độ dài hai cạnh còn lại sẽ là 4cm và 5cm

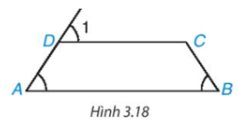
Ta có \(\widehat A = \widehat {{D_1}}\) mà hai góc này ở vị trí đồng vị nên AB // CD.
Suy ra tứ giác ABCD là hình thang.
Mặt khác hình thang ABCD có \(\widehat A = \widehat B\) nên ABCD là hình thang cân.
Do đó AD = BC (đpcm).

Độ dài các cạnh của tứ giác ABCD bằng nhau