Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

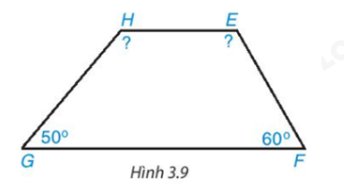
Áp dụng định lí tổng bốn góc trong một tứ giác vào tứ giác HEFG, ta có:
\(\widehat H + \widehat E + \widehat F + \widehat G = {360^o}\)
\(\widehat E\)+10°+\(\widehat E\)+60°+50°=360o
2\(\widehat E\)+120°=360°
Suy ra 2\(\widehat E\)=360°−120°=240°
Khi đó \(\widehat E\)=120°
Suy ra \(\widehat H\)=\(\widehat E\)+10°=120°+10°=130°
Vậy \(\widehat H\)=130°; \(\widehat E\)= 120°

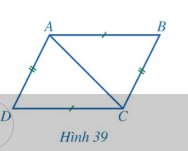
a) Nối AC, BD (như hình vẽ
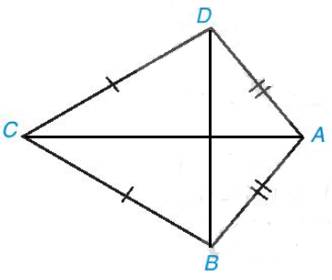
Ta có AB = AD hay hai điểm A cách đều hai đầu mút B và D;
CB = CD hay hai điểm C cách đều hai đầu mút B và D;
Do đó, hai điểm A và C cách đều hai đầu mút B và D.
Vậy AC là đường trung trực của đoạn thẳng BD.
b) Gọi I là giao điểm của AC và BD.
Vì AC là đường trung trực của đoạn thẳng BD nên AC ⊥ BD.
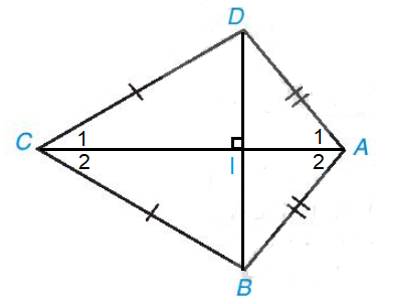
• Xét tam giác ABD cân tại A (vì AB = AD) có AI là đường cao (vì AI ⊥ BD)
Nên AI cũng là tia phân giác của \(\widehat {BA{\rm{D}}}\) hay \(\widehat {{A_1}} = \widehat {{A_2}}\)
Suy ra \(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {B{\rm{D}}A}:2 = {100^o}:2 = {50^o}\)
• Xét tam giác BCD cân tại C (vì BC = CD) có CI là đường cao (vì AC ⊥ BD)
Nên CI cũng là tia phân giác của \(\widehat {BC{\rm{D}}}\) hay \(\widehat {{C_1}} = \widehat {{C_2}}\)
Suy ra \(\widehat {{C_1}} = \widehat {{C_2}} = \widehat {BC{\rm{D}}}:2 = {60^o}:2 = {30^o}\)
• Xét tam giác ACD có: \(\widehat {{A_1}} + \widehat {{C_1}} + \widehat {A{\rm{D}}C} = {180^o}\) (định lí tổng ba góc trong một tam giác).
Hay 50°+30°+\(\widehat {A{\rm{D}}C}\)=180°
Suy ra \(\widehat {A{\rm{D}}C}\)=180°−50°−30°=100°
Xét tứ giác ABCD có:
\(\widehat {BA{\rm{D}}} + \widehat {ABC} + \widehat {BC{\rm{D}}} + \widehat {A{\rm{D}}C} = {360^o}\)(định lí tổng bốn góc của một tứ giác).
Hay 100°+\(\widehat {ABC}\)+60°+100°=360°
Suy ra \(\widehat {ABC}\)+260°=360o
Do đó \(\widehat {ABC}\)=360°−260°=100o
Vậy \(\widehat {ABC}\)=100° ;\(\widehat {A{\rm{D}}C}\)=100°

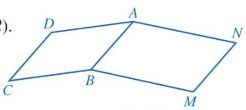
a, Do ABCD là hình bình hành: AB = CD.
Do ABMN là hình bình hành: AB = MN
Suy ra: CD = MN = AB
b, Do ABCD là hình bình hành \( \Rightarrow \widehat {BCD} = \widehat {DAB}\)
Do ABMN là hình bình hành \( \Rightarrow \widehat {BMN} = \widehat {NAB}\)
\(\widehat {BCD} + \widehat {BMN} = \widehat {DAB} + \widehat {NAB} = \widehat {DAN}\)

a) Vì ABCD là hình bình hành nên AB // CD; AD // BC.
Suy ra \(\widehat {BAC} = \widehat {AC{\rm{D}}};\widehat {BCA} = \widehat {DAC}\)(hai góc so le trong).
Xét ∆ABC và ∆CDA có:
\(\widehat {BAC} = \widehat {AC{\rm{D}}}\) (chứng minh trên);
Cạnh AC chung.
\(\widehat {BCA} = \widehat {DAC}\) (chứng minh trên);
Do đó ∆ABC = ∆CDA (g.c.g).
Suy ra AB = CD, AD = BC (các cặp cạnh tương ứng); \(\widehat {ABC} = \widehat {C{\rm{D}}A}\) (hai góc tương ứng).
b) Xét ∆ABD và ∆CDB có:
AB = CD (chứng minh trên);
AD = BC (chứng minh trên);
Cạnh BD chung.
Do đó ∆ABD = ∆CDB.
Suy ra \(\widehat {DAB} = \widehat {BC{\rm{D}}}\) (hai góc tương ứng).
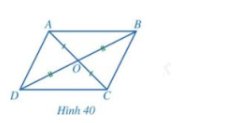
c) Xét ∆AOB và ∆COD có:
\(\widehat {BAC} = \widehat {AC{\rm{D}}}\) (chứng minh trên);
AB = CD (chứng minh trên);
\(\widehat {BCA} = \widehat {DAC}\) (chứng minh trên);
Do đó ∆AOB = ∆COD (g.c.g).
Suy ra OA = OC, OB = OD (các cặp cạnh tương ứng).

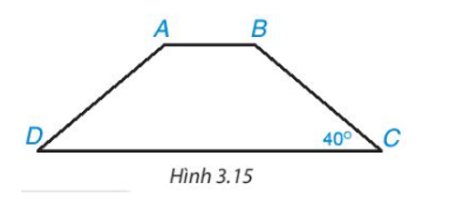
Hình thang cân ABCD (AB //CD) nên ta có:
\(\widehat A = \widehat B;\widehat C = \widehat D = {40^o}\)
\(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
Khi đó: \(\widehat A + \widehat A + {40^o} + {40^o} = {360^o}\)
Hay: \(2\widehat A + {80^o} = {360^o}\)
Suy ra: \(2\widehat A = {360^o} - {80^o} = {280^o}\)
Do đó: \(\widehat A = {140^o}\) nên \(\widehat B = {140^o}\)
Vậy: \(\widehat A = {140^o};\widehat B = {140^o};\widehat C = {40^o};\widehat D = {40^o}\)

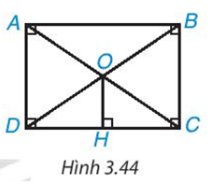
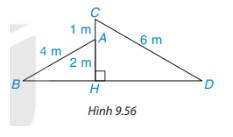
Xét tam giác DBC, ta có:
O là trung điểm cạnh BD (tính chất hình chữ nhật)
OH // BC (cùng vuông góc với CD)
⇒ OH là đường trung bình tam giác BCD.
⇒ H là trung điểm của CD (đpcm).

a) Xét hai tam giác ABC và CDA có:AB = CD; AD = BC; AC chung nên \(\Delta ABC = \Delta C{\rm{D}}A(c - c - c)\)
Suy ra: \(\widehat {BAC}\) = \(\widehat {DCA};\widehat {ACB}\) = \(\widehat {CAD}\).
Nên ABCD hình bình hành.
b) Xét hai tam giác ABO và tam giác CDO có: \(OA = OB;\widehat {AOB} = \widehat {CO{\rm{D}}};OC = O{\rm{D}}\)
Suy ra: \(\Delta ABO = \Delta C{\rm{D}}O\)
Suy ra: \(\widehat {BAC}\) = \(\widehat {DCA};\widehat {ACB}\) = \(\widehat {CA{\rm{D}}}\).
Nên ABCD là hình bình hành.

Xét hai tam giác vuông HBA và tam giác vuông HDC nhận thấy:
\(\frac{{AB}}{{C{\rm{D}}}} = \frac{{AH}}{{CH}} = \frac{2}{3}\)
=> Hai tam giác đồng dạng
\( \Rightarrow \widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\)

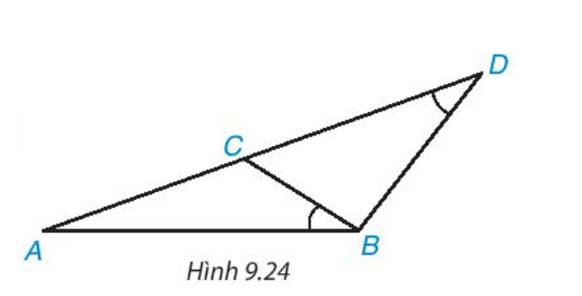
Xét tam giác ABC và tam giác ADB có
\(\widehat {ABC} = \widehat {A{\rm{D}}B}\) và \(\widehat A\) chung
=> ΔABC ∽ ΔADB (g.g)
=> \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AB}}\)
=> \(A{B^2} = A{\rm{D}}.AC\)
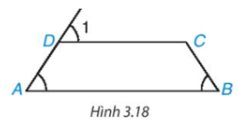

Ta có \(\widehat A = \widehat {{D_1}}\) mà hai góc này ở vị trí đồng vị nên AB // CD.
Suy ra tứ giác ABCD là hình thang.
Mặt khác hình thang ABCD có \(\widehat A = \widehat B\) nên ABCD là hình thang cân.
Do đó AD = BC (đpcm).