Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Đổi 2 năm là 24 tháng. Lãi suất 6%/năm tương ứng với $0,5$ %/tháng
Giả sử phải gửi $x$ (triệu đồng)
Ta có: $x(1+\frac{0,5}{100})^{24}=500$
$\Rightarrow x=\frac{500}{1,005^{24}}=443,6$ (triệu đồng)
$\Rightarrow x=\frac{500}{1,06^2}=445$ (triệu đồng)

Đáp án A
Phương pháp:
Công thức lãi kép, không kỳ hạn: An = M(1 + r%)n
Với:
An là số tiền nhận được sau tháng thứ n,
M là số tiền gửi ban đầu,
n là thời gian gửi tiền (tháng),
r là lãi suất định kì (%)
Cách giải:
Số tiền ông An rút lần 1 là: 100.(1 + 8%)5 = 146,9328077 (triệu đồng)
Số tiền ông An gửi lần 2 là: 146.9328077 : 2 = 73,46640384 (triệu đồng)
Số tiền ông An rút lần 2 (gửi 5 năm tiếp theo) là:
73,46640384.(1 + 8%)5 = 107,9462499 (triệu đồng)
Số tiền lãi là: 107,9462499 - 73,4660384 = 34,47984602 ≈ 34,480 (triệu đồng).

Chọn A.
Ta có: T = A(1+ r)n
- 12 tháng đầu: lãi suất 1%/ tháng suy ra r1= 3%/quý và n = 4
Do đó sau 12 tháng đầu tiên số tiền cả gốc lẫn lãi là:T1 = 2( 1 + 3%) 4
- 18 tháng tiếp theo: lãi suất 1,1%/tháng suy ra r2= 3,3%/ quý và
Do đó sau 18 tháng tiếp theo số tiền cả gốc lẫn lãi là:T2 = T1( 1 + 3,3%)6
- 6 tháng cuối cùng: lãi suất 1,2%/ tháng suy rar3= 3,6%/ quý và n = 2
Số tiền cả gốc lẫn lãi thu được là T3= T2( 1+ 3,6%) 2 = 2,9356.

Tiền lãi sau một tháng là:
5 000 0000 x 0,5 : 100 = 25 000 (đồng)
Cả tiền gửi và tiền lãi suất sau một tháng là:
5 000 000 + 25 000 = 5 025 000 (đồng).
Đáp án: 5 025 000 (đồng).
sửa số đo
Một tháng lãi được số tiền là
42 965 600 x 0,5% = 214828 (đồng)
Tổng cả gốc lẫn lãi là
42 965 600 + 214 828 = 43 180 428 (đồng)
HT




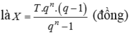
Chọn A.
Ta có: T = A(1 + r) n trong đó n là số kỳ hạn, r là lãi suất theo kỳ hạn
TH1: r = 1%/tháng và n = 12 khi đó T1 = A(1 + 0,01)12
TH2: r = 3%/tháng và n = 4 khi đó T2 = A(1 + 0,03)4
TH3: r = 6%/tháng và n = 2 khi đó T3 = A(1 + 0,06)2
TH4: r = 12%/tháng và n = 1 khi đó T4 = A(1 + 0,12)
Từ 4 kết quả trên bạn A nên chọn phương án gửi theo kỳ hạn 1 tháng để có số tiền là lớn nhất.