
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


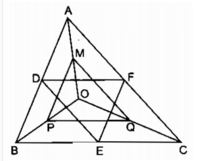
Lục giác DPEQFM có các cặp cạnh đối bằng nhau từng đôi một:
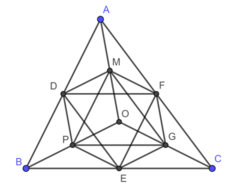
DP = QF (vì bằng 1/2 OA);
PE = MF (vì bằng 1/2 OC)
EQ = MD (vì bằng 1/2 OB)
Lục giác DPEQFM có 6 cạnh bằng nhau chỉ khi DP = PE = EQ.
Muốn vậy, ta phải có OA = OB = OC, khi đó O là điểm cách đều ba điểm A, B, C. Vậy O là giao điểm của ba đường trung trực tam giác ABC.

A B C D E G F I K
a. Xét \(\Delta ABC\)
Ta có \(\hept{\begin{cases}AE=EB\\AD=DC\end{cases}\Rightarrow DE}\)là đường trung bình của tam giác ABC
\(\Rightarrow\)DE song song BC và \(DE=\frac{1}{2}BC\left(1\right)\)
Xét \(\Delta BGC\)có \(\hept{\begin{cases}BI=IG\\CK=KG\end{cases}\Rightarrow IK}\)là đường trung bình của tam giác BGC
\(\Rightarrow\)IK song song BC và \(IK=\frac{1}{2}BC\left(2\right)\)
Từ (1) và (2) \(\Rightarrow DE\)song song \(IK\)và \(DE=IK\)
b. Theo tính chất của trọng tâm ta có
\(GF=\frac{1}{3}AF\);\(AG=\frac{2}{3}AF\left(3\right)\)
Xét \(\Delta ABG\)có IE là đường trung bình suy ra \(IE=\frac{1}{2}AG\left(4\right)\)
Từ (3) và (4) \(\Rightarrow IE=\frac{1}{2}AG=\frac{1}{2}.\frac{2}{3}AF=\frac{1}{3}AF=GF\)
Vậy \(IE=GF\)

Từ M kẻ MK//DE ,MKcắt AC tại K
Xét tg AMK có:
DE//MK
D là tr.điểm AM
=>E là tr.điểm AK
=>AE=EK=1/2AK
Xét tg BEC có:
BE//MK (do DE//MK)
M là tr.điểm BC (AM là tr.tuyến của tg ABC)
=>K là tr.điểm EC
=>KE=1/2EC
Mà AE=EK (cmt)
=>AE=1/2EC (đpcm)

Trường hợp 1: Đường thẳng d song song với BC.
Theo định lý Ta - lét ta có:\(\frac{BE}{EA}=\frac{OD}{OA}\frac{CD}{FA}=\frac{OD}{OA}\)
Suy ra : \(\frac{BE}{AE}+\frac{CF}{AF}=1\Leftrightarrow\frac{OD}{OA}+\frac{OD}{OA}=1\Leftrightarrow2OD=OA\left(1\right)\)
TRƯỜNG HỢP 2 LÀM TƯƠNG TỰ NHA :D


A B C T H U
A D B C E G