Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Diện tích xung quanh hình nón:
$\pi (r+R).l=\pi (6+3).4=36\pi$ (cm vuông)
Diện tích toàn phần:
$36\pi+\pi r^2+\pi R^2=36\pi +\pi.3^2+\pi. 6^2=81\pi$ (cm vuông)
Thể tích:
Chiều cao hình nón: $\sqrt{4^2-(6-3)^2}=\sqrt{7}$ (cm)
$\frac{1}{3}\pi (r^2+R^2+r.R)h=\frac{1}{3}\pi (3^2+6^2+3.6).\sqrt{7}=21\sqrt{7}\pi$ (cm khối)

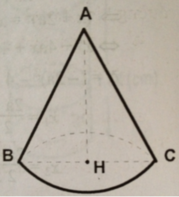
Hình vẽ đâu bn.(không có hình thì mik ko bt AB là đường sinh hay chiều cao nhé. Nhưng thường thì AB là đường sinh)
(nếu đề bài AB là đường cao thì bn đăng lại nhé)
\(Sxq=\pi\left(r+R\right)l=\pi\left(3+6\right)4=36\pi\left(cm^2\right)\)
\(Stp=\pi\left(r+R\right)l+\pi\left(r^2+R^2\right)=36\pi+\pi\left(3^2+6^2\right)=36\pi+45\pi\)
\(=81\pi\left(cm^2\right)\)
có: \(h=\sqrt{l^2-\left(R-r\right)^2}=\sqrt{4^2-\left(6-3\right)^2}=\sqrt{7}cm\)
\(V=\dfrac{1}{3}\pi\left(r^2+R^2+rR\right).h\)\(=\dfrac{1}{3}\pi.\left(3^2+6^2+3.6\right).\sqrt{7}=21\sqrt{7}.\pi\left(cm^3\right)\)

Tham khảo
a, V = 9706 π cm 3 ≈9,71
b, S = π (81+23√554) ≈622,36


Lời giải:
Diện tích vải cần dùng để làm đèn là diện tích xung quanh cộng với diện tích đáy nhỏ
$S=S_{xq}+S_{đáy nhỏ}=\pi (R+r)l+\pi r^2=\pi (30+20).40+\pi .20^2=2400\pi$ (cm2)