Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
Độ dịch chuyển có độ lớn bằng diện tích của hình thang vuông có đường cao là t và các đáy có độ lớn v0, v.
Từ đồ thị ta có: \(\left\{ \begin{array}{l}{v_0} = 4\left( {m/s} \right);v = 16\left( {m/s} \right)\\t = 6\left( s \right)\end{array} \right.\)
Suy ra: Độ dịch chuyển là:
\(d = \frac{{\left( {4 + 16} \right).6}}{2} = 60\left( m \right)\)
2.
Ta có: Gia tốc: \(a = \frac{{\Delta v}}{{\Delta t}}\)
Từ đồ thị ta thấy: Độ biến thiên vận tốc các khoảng thời gian bằng nhau là 2 m/s.
Xét giữa 2 thời điểm A và B:
=> \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{{v_B} - {v_A}}}{{{t_A} - {t_B}}} = \frac{{12 - 10}}{{4 - 3}} = \frac{2}{1} = 2(m/{s^2})\)
Vậy có thể xác định được giá trị của gia tốc dựa trên đồ thị v – t.

Giải:
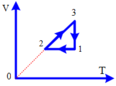
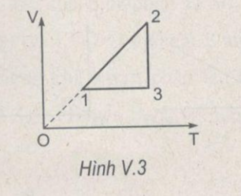
(1) đến (2) là quá trình đẳng tích, T giảm, p giảm
(2) đến (3) là quá trình đẳng áp, T tăng, V tăng
(3 ) đến (1) là quá trình đẳng nhiệt, V giảm, p tăng
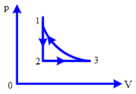

đẳng nhiệt
\(p_1.V_1=p_2.V_2\)
\(\Leftrightarrow p_2=\)\(3,75.10^5Pa\)
(hình xem trong sách giáo khoa trang 158 có ấy)

Xem hình V.2G
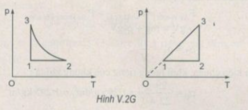
Quá trình (2-3) là đẳng nhiệt
Quá trình (3-1) là đẳng tích
Quá trình (1-2) là đẳng áp

1.
Lập bảng ghi số liệu.
Độ dịch chuyển (m) | 0 | 200 | 400 | 600 | 800 | 1000 | 800 |
Thời gian (s) | 0 | 50 | 100 | 150 | 200 | 250 | 300 |
2.
Vẽ đồ thị:
Từ bảng số liệu ta vẽ được đồ thị như hình sau:


gọi số lần bơm là x (lần)
trạng thái 1:V1=0,1x(l) P1=1000000(pa)
trạng thái2: V2=2(l) Pa2=2000000(pa)
theo bôi- lơ..=>x=40

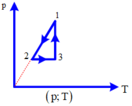
Đường biểu diễn sự biến thiên của p theo V trong hệ toạ độ (p;V) là một đường hypebol