Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
a) Vẽ đồ thị độ dịch chuyển – thời gian:
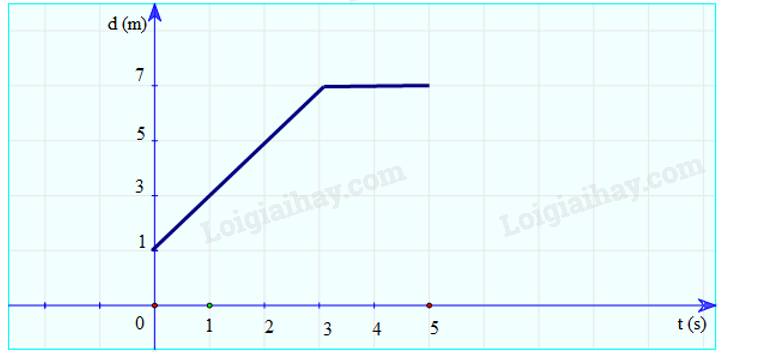
b) Mô tả chuyển động của xe:
- Từ 0 – 3 giây: xe chuyển động thẳng.
- Từ giây thứ 3 đến giây thứ 5: xe đứng yên (dừng lại)
c) Độ dịch chuyển của xe trong 3 giây đầu là:
\(d = 7 - 1 = 6m\)
Vận tốc của xe trong 3 giây đầu là:
\(v = \frac{{\Delta d}}{{\Delta t}} = \frac{6}{3} = 2\left( {m/s} \right)\)
2.
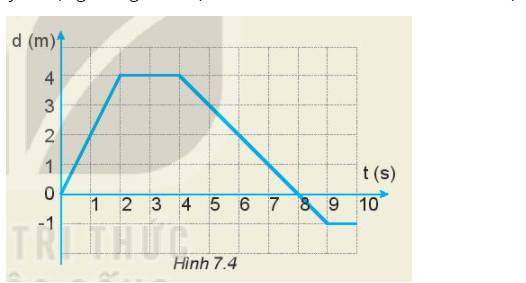
a) Mô tả chuyển động của xe:
- Trong 2 giây đầu: xe chuyển động thẳng
- Từ giây thứ 2 đến giây thứ 4: xe đứng yên
- Từ giây thứ 4 đến giây thứ 10: xe chuyển động thẳng theo chiều ngược lại.
- Từ giây thứ 9 đến giây thứ 10: xe dừng lại.
b)
- Ở giây thứ 2: xe ở vị trí cách điểm xuất phát 4 m.
- Ở giây thứ 4: xe ở vị trí cách điểm xuất phát 4 m
- Ở giây thứ 8: xe trở về vị trí xuất phát
- Ở giây thứ 10: xe ở vị trí cách điểm xuất phát 1 m theo chiều âm
c) Xác định tốc độ và vận tốc của xe:
- Trong 2 giây đầu, xe chuyển động thẳng, không đổi chiều nên tốc độ bằng vận tốc:
\(v = \frac{d}{t} = \frac{4}{2} = 2\left( {m/s} \right)\)
- Từ giây 2 đến giây 4: xe đứng yên nên vận tốc và tốc độ của xe đều bằng 0.
- Từ giây 4 đến giây 8:
+ Tốc độ: \(v = \frac{s}{t} = \frac{4}{4} = 1\left( {m/s} \right)\)
+ Vận tốc: \(v = \frac{{\Delta d}}{{\Delta t}} = \frac{{0 - 4}}{{8 - 4}} = - 1\left( {m/s} \right)\)
d)
- Từ đồ thị, ta thấy quãng đường đi được của xe sau 10 giây chuyển động là:
\(s = 4 + 4 + 1 = 9\left( m \right)\)
- Độ dịch chuyển của xe sau 10 giây là:
\(d = - 1 - 4 + 4 = - 1\left( m \right)\)
=> Quãng đường và độ dịch chuyển của xe sau 10 giây không giống nhau vì xe chuyển động theo 2 chiều.

a) Giá trị trung bình của thời gian rơi là:
\(\begin{array}{l}
\bar t = \frac{{{t_1} + {t_2} + {t_3} + {t_4} + {t_5}}}{5}\\
\Rightarrow \overline t = \frac{{0,2027 + 0,2024 + 0,2023 + 0,2023 + 0,2022}}{5} \approx 0,2024(s)
\end{array}\)
b)
- Sai số tuyệt đối ứng với 5 lần đo là:
+ Lần đo 1: \(\Delta {t_1} = \left| {\overline t - {t_1}} \right| = \left| {0,2024 - 0,2027} \right| = {3.10^{ - 4}}(s)\)
+ Lần đo 2: \(\Delta {t_2} = \left| {\overline t - {t_2}} \right| = \left| {0,2024 - 0,2024} \right| = 0(s)\)
+ Lần đo 3: \(\Delta {t_3} = \left| {\overline t - {t_3}} \right| = \left| {0,2024 - 0,2023} \right| = {10^{ - 4}}(s)\)
+ Lần đo 4: \(\Delta {t_4} = \left| {\overline t - {t_4}} \right| = \left| {0,2024 - 0,2023} \right| = {10^{ - 4}}(s)\)
+ Lần đo 5: \(\Delta {t_5} = \left| {\overline t - {t_5}} \right| = \left| {0,2024 - 0,2022} \right| = {2.10^{ - 4}}(s)\)
- Sai số tuyệt đối trung bình của phép đo thời gian là:
\(\overline {\Delta t} = \frac{{\Delta {t_1} + \Delta {t_2} + \Delta {t_3} + \Delta {t_4} + \Delta {t_5}}}{5} = \frac{{{{3.10}^{ - 4}} + 0 + {{2.10}^{ - 4}} + {{2.10}^{ - 4}} + {{10}^{ - 4}}}}{5} = 1,{6.10^{ - 4}}(s)\)

| Công thức | Chuyển động thẳng đều | Chuyển động thẳng biến đổi đều | Chuyển động rơi tự do | Chuyển động ném ngang |
| Vận tốc | \(v=\frac{s}{t}\) | \(v=v_0+at\) | \(v=gt\) | \(v=\sqrt{v_0^2+g^2t^2}\) |
| Quãng đường (hoặc tầm bay xa) | \(s=vt\) | \(s=v_0t+\frac{1}{2}at^2\) | \(s=\frac{1}{2}gt^2\) | \(L=v_0\sqrt{\frac{2h}{g}}\) |
| Gia tốc | \(a=0\text{ m/s}^2\) | \(a=\frac{v-v_0}{t}\) | \(g\approx9,8\text{ m/s}^2\) | \(g\approx9,8\text{ m/s}^2\) |
| Thời gian chuyển động | \(t=\frac{s}{v}\) | \(----\) | \(t=\sqrt{\frac{2h}{g}}\) | \(t=\sqrt{\frac{2h}{g}}\) |

1.
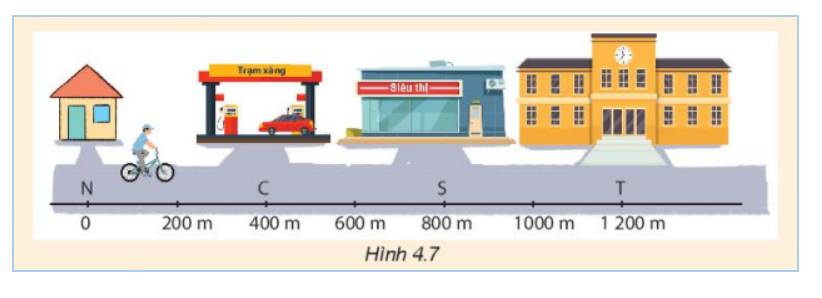
a) Quãng đường bạn A đi từ trạm xăng đến siêu thị là: 800 – 400 = 400 (m)
Độ dịch chuyển của bạn A từ trạm xăng đến siêu thị là: 800 – 400 = 400 (m)
b) Quãng đường đi được của bạn A trong cả chuyến đi:
+ Quãng đường bạn A đi từ nhà đến siêu thị là: 800 m
+ Quãng đường bạn A quay về nhà cất đồ là: 800 m
+ Quãng đường bạn A đi từ nhà đến trường là: 1200 m
=> Quãng đường đi được của bạn A trong cả chuyến đi là: 800 + 800 + 1200 = 2800 (m)
Điểm đầu xuất phát của bạn A là nhà, điểm cuối của bạn A là trường
=> Độ dịch chuyển của bạn A là 1200 m.
2.
Chuyển động | Quãng đường đi được s (m) | Độ dịch chuyển d (m) |
Từ trạm xăng đến siêu thị | sTS = 400 | dTS = 400 |
Cả chuyến đi | s = 2800 | d = 1200 |
3.
Dự đoán trong câu hỏi 2 cuối trang 23 là độ dịch chuyển và quãng đường đi được bằng nhau khi vật chuyển động thẳng, không đổi chiều
Từ bảng kết quả ta thấy dự đoán trên là đúng.
1.
Lập bảng ghi số liệu.
Độ dịch chuyển (m)
0
200
400
600
800
1000
800
Thời gian (s)
0
50
100
150
200
250
300
2.
Vẽ đồ thị:
Từ bảng số liệu ta vẽ được đồ thị như hình sau: