LN
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
PT
1
5 tháng 2 2021
\(x^2+3x+4=0\)
\(\Leftrightarrow x^2+2.x.\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{7}{4}=0\)
\(\Leftrightarrow\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}=0\)
\(\Leftrightarrow\left(x+\dfrac{3}{2}\right)^2=-\dfrac{7}{4}\left(VL\right)\)
Vậy ĐPCM
MH
5 tháng 2 2021
\(x^2+3x+4=0\Leftrightarrow x^2+2.x.\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{7}{4}=0\)
\(\Leftrightarrow x^2+2.x.\dfrac{3}{2}+\left(\dfrac{3}{2}\right)^2+\dfrac{7}{4}=0\Leftrightarrow\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}=0\)
Ta có \(\left(x+\dfrac{3}{2}\right)^2\ge0,\forall x\)
\(\Rightarrow\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}>0,\forall x\)
Vậy phương trình vô nghiệm.
KV
17 tháng 3 2023
x² + 2x + 3
= x² + 2x + 1 + 2
= (x + 1)² + 2 > 0 với mọi x
Vậy phương trình đã cho vô nghiệm
18 tháng 1 2022
a:
Thay x=2 vào (1), ta được:
\(2^2-5\cdot2+6=0\)(đúng)
Thay x=2 vào (2), ta được:
\(2+\left(2-2\right)\cdot\left(2\cdot2+1\right)=2\)(đúng)
b: (1)=>(x-2)(x-3)=0
=>S1={2;3}
(2)=>\(x+2x^2+x-4x-2-2=0\)
\(\Leftrightarrow x^2+x-2=0\)
=>(x+2)(x-1)=0
=>S2={-2;1}
vậy: x=3 là nghiệm của (1) nhưng không là nghiệm của (2)
12 tháng 4 2022
\(x^2-x+2=0\)
\(\Leftrightarrow x^2-x+\dfrac{1}{4}+\dfrac{3}{4}=0\)
\(\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\) (vô lý)
=> Phương trình vô nghiệm
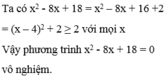
\(x^2\ge0\Rightarrow x^2+1\ge1\Rightarrowđpcm\)
x2+1=0
<=> x2=-1
<=> \(x=\sqrt{-1}\)
Vế trái vô lý. => đpcm