Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

y’ = -x2 - 1 < 0, ∀x ∈ R
Hàm số luôn nghịch biến trên tập xác định. Do đó hàm số không có cực trị.
Chọn đáp án B

Ta có: 1 + x = 0 ⇔ x = -1
limx→−1−y=+∞,limx→−1+y=−∞limx→−1−y=+∞,limx→−1+y=−∞. Tiệm cận đứng x = -1
limx→±∞y=−1limx→±∞y=−1. Tiệm cận ngang y = 1
Vậy đồ thị có 2 tiệm cận. Chọn đáp án B

y’ = x² – 4x + 3 = 0 ⇔ x =1, x = 3 y” = 2x – 4, y”(1) = -2, y”(3) = 2 Suy ra hàm số đạt cực tiểu tại x = 3. Phương trình tiếp tuyến tại điểm cực tiểu có hệ số góc là y'(3) = 0. Do đó, tiếp tuyến song song với trục hoành. Chọn B

a) y = f(x) = x3 – 3mx2 + 3(2m-1)x + 1
Tập xác định: D = R
y’= 3x2 -6mx + 3(2m-1) = 3(x2 – 2mx + 2m – 1)
Hàm số đồng biến trên D = R ⇔ y’ ≥ 0, ∀x ∈ R
⇔ x2 – 2mx + 2m - 1≥0, ∀x ∈ R
⇔ Δ’ = m2 – 2m + 1 = (m-1)2 ≤ 0 ⇔ m =1
b) Hàm số có một cực đại và một cực tiểu
⇔ phương trình y’= 0 có hai nghiệm phân biệt
⇔ (m-1)2 > 0 ⇔ m≠1
c) f’’(x) = 6x – 6m > 6x
⇔ -6m > 0 ⇔ m < 0

bạn trả lời từng câu cũng được mà :) làm được câu nào thì giúp mình nhé. Tks!

- Xét a = 0 hàm số trở thành y = -9x + b. Trường hợp này hàm số không có cực trị.
- Xét a # 0. Ta có : y’ = 5a2x2 + 4ax – 9 ; y’= 0 ⇔ hoặc
- Với a < 0 ta có bảng biến thiên :
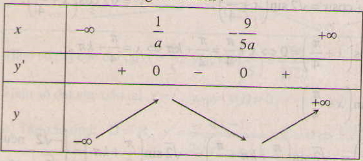
Theo giả thiết là điểm cực đại nên
. Theo yêu cầu bài toán thì
- Với a > 0 ta có bảng biến thiên :
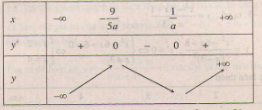
Vì là điểm cực đại nên
. Theo yêu cầu bài toán thì:
Vậy các giá trị a, b cần tìm là: hoặc
.

a) Tập xác định: D = R\{m}
Hàm số đồng biến trên từng khoảng (−∞;m),(m;+∞)(−∞;m),(m;+∞)khi và chỉ khi:
y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2
b) Tập xác định: D = R\{m}
Hàm số nghịch biến trên từng khoảng khi và chỉ khi:
y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0
[m<1m>4[m<1m>4
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3
d) Tập xác định: D = R
Hàm số đồng biến trên R khi và chỉ khi:
y′=3x2−4mx+12≥0⇔′=4m2−36≤0⇔m2≤9⇔−3≤m≤3

Câu 1: Xét trên miền [1;4]
Do \(f\left(x\right)\) đồng biến \(\Rightarrow f'\left(x\right)\ge0\)
\(x\left(1+2f\left(x\right)\right)=\left[f'\left(x\right)\right]^2\Leftrightarrow x=\frac{\left[f'\left(x\right)\right]^2}{1+2f\left(x\right)}\Leftrightarrow\frac{f'\left(x\right)}{\sqrt{1+2f\left(x\right)}}=\sqrt{x}\)
Lấy nguyên hàm 2 vế:
\(\int\frac{f'\left(x\right)dx}{\sqrt{1+2f\left(x\right)}}=\int\sqrt{x}dx\Leftrightarrow\int\left(1+2f\left(x\right)\right)^{-\frac{1}{2}}d\left(f\left(x\right)\right)=\int x^{\frac{1}{2}}dx\)
\(\Leftrightarrow\sqrt{1+2f\left(x\right)}=\frac{2}{3}x\sqrt{x}+C\)
Do \(f\left(1\right)=\frac{3}{2}\Rightarrow\sqrt{1+2.\frac{3}{2}}=\frac{2}{3}.1\sqrt{1}+C\Rightarrow C=\frac{4}{3}\)
\(\Rightarrow\sqrt{1+2f\left(x\right)}=\frac{2}{3}x\sqrt{x}+\frac{4}{3}\)
Đến đây có thể bình phương chuyển vế tìm hàm \(f\left(x\right)\) chính xác, nhưng dài, thay luôn \(x=4\) vào ta được:
\(\sqrt{1+2f\left(4\right)}=\frac{2}{3}4.\sqrt{4}+\frac{4}{3}=\frac{20}{3}\Rightarrow f\left(4\right)=\frac{\left(\frac{20}{3}\right)^2-1}{2}=\frac{391}{18}\)
Câu 2:
Diện tích hình phẳng cần tìm là hai miền đối xứng qua Oy nên ta chỉ cần tính trên miền \(x\ge0\)
Hoành độ giao điểm: \(sinx=x-\pi\Rightarrow x=\pi\)
\(S=2\int\limits^{\pi}_0\left(sinx-x+\pi\right)dx=4+\pi^2\Rightarrow\left\{{}\begin{matrix}a=4\\b=1\end{matrix}\right.\)
\(\Rightarrow2a+b^3=9\)

Tập xác định của hàm số : D = R\{-3}
\(y'=\dfrac{11}{\left(x+3\right)^2}>0\forall x\in D\)
Hàm số đồng biến trên tập xác định.
Vậy chọn đáp án D.
Tập xác định của hàm số: D = R\ {-3}
Hàm số đồng biến trên tập xác định
Chọn đáp án D