Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Ta có: y’ = cos 3x + mcos x
Hàm số đạt cực đại tại
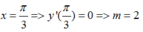
m = 2 => y’ = cos 3x + 2cos x => y’’ = -3sin 3x – 2sin x
=>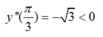
Vậy, m = 2

Đề đúng là \(y=mx^2+2\left(m^2-5\right)x^4+4\) chứ bạn (nghĩa là ko bị nhầm lẫn vị trí \(x^2\) và \(x^4\))
Hàm có đúng 2 điểm cực đại và 1 điểm cực tiểu khi:
\(\left\{{}\begin{matrix}2\left(m^2-5\right)< 0\\2\left(m^2-5\right).m< 0\end{matrix}\right.\)
\(\Leftrightarrow0< m< \sqrt{5}\)
\(\Rightarrow\) có 2 giá trị nguyên của m thỏa mãn

Chọn C.
![]()
![]()
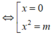
Đồ thị hàm số có 3 điểm cực trị ⇔ m > 0
Khi đó, tọa độ ba điểm cực trị là
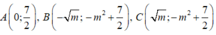
O là trực tâm tam giác
![]()

![]()
![]()
![]()
![]()
Vậy, chọn phương án C.

Ta có đạo hàm y’ = 4x3- 4( 1-m2) x
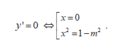
Hàm số có cực đại , cực tiểu khi và chỉ khi -1< m <1
Tọa độ điểm cực trị
A ( 0 ; m + 1 ) ; B ( 1 - m 2 ; - m 4 + 2 m 2 + m ) ; C ( - 1 - m 2 ; - m 4 + 2 m 2 + m ) ; B C → = ( - 2 ( 1 - m 2 ; 0 )
Phương trình đường thẳng BC: y+ m4- 2m2- m=0
d( A: BC) = m4-2m2+ 1,
B C = 2 1 - m 2 ⇒ S ∆ A B C = 1 2 B C . d A , B C = 1 - m 2 ( m 4 - 2 m 2 + 1 ) = ( 1 - m 2 ) 5 ≤ 1
Vậy S đạt giá trị lớn nhất khi và chỉ khi m= 0.
Chọn D.

\(y=x^4-2\left(m^2-m+1\right)x+m-1\)
\(y'=4x^3-4\left(m^2-m+1\right)x\)
\(y'=0\Leftrightarrow4x^3-4\left(m^2-m+1\right)x=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm\sqrt{m^2-m+1}\end{cases}}\)
Khoảng cách giữa hai điểm cực tiểu là:
\(2\sqrt{m^2-m+1}=2\sqrt{\left(m-\frac{1}{2}\right)^2+\frac{3}{4}}\ge2\sqrt{\frac{3}{4}}\)
Dấu \(=\)khi \(m-\frac{1}{2}=0\Leftrightarrow m=\frac{1}{2}\).
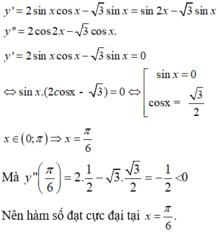

Đáp án C