
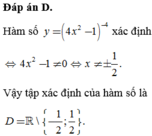
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

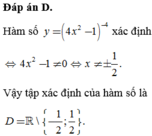

Chọn D
Hàm số xác định với mọi ![]() thì
thì  luôn đúng với mọi
luôn đúng với mọi ![]()
+) Ta có: ![]()
![]()
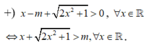
Xét hàm số ![]()
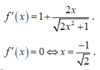
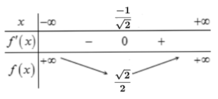
Từ bảng biến thiên ta thấy để 
Kết hợp điều kiện
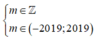
![]()
Kết luận: có 2019 giá trị của m thỏa mãn bài toán.

`a)TXĐ: R`
`b)TXĐ: R\\{0}`
`c)TXĐ: R\\{1}`
`d)TXĐ: (-oo;-1)uu(1;+oo)`
`e)TXĐ: (-oo;-1/2)uu(1/2;+oo)`
`f)TXĐ: (-oo;-\sqrt{2})uu(\sqrt{2};+oo)`
`h)TXĐ: (-oo;0) uu(2;+oo)`
`k)TXĐ: R\\{1/2}`
`l)ĐK: {(x^2-1 > 0),(x-2 > 0),(x-1 ne 0):}`
`<=>{([(x > 1),(x < -1):}),(x > 2),(x ne 1):}`
`<=>x > 2`
`=>TXĐ: (2;+oo)`
câu l) $x^2-1 > 0$ thì giải ra 2 nghiệm $x < -1, x > 1$ mới đúng chứ nhỉ?

\(y'_1=-\dfrac{2}{\left(x-1\right)^2}\) nghịch biến trên R/{1}
\(y'_2=-3x^2+2x-3\) có nghiệm khi y' = 0
\(y'_3=4x^3+4x\) có nghiệm khi y' = 0
Vậy không có hàm số đơn điệu trên R.
đơn điệu trên R là sao bạn? bạn chỉ mk cách nhận bt đc ko?

d: ĐKXĐ: \(x^2-1< >0\)
=>\(x^2\ne1\)
=>\(x\notin\left\{1;-1\right\}\)
Vậy: TXĐ là D=R\{1;-1}
b: ĐKXĐ: \(2-x^2>0\)
=>\(x^2< 2\)
=>\(-\sqrt{2}< x< \sqrt{2}\)
Vậy: TXĐ là \(D=\left(-\sqrt{2};\sqrt{2}\right)\)
a: ĐKXĐ: \(x-1>0\)
=>x>1
Vậy: TXĐ là \(D=\left(1;+\infty\right)\)
c: ĐKXĐ: \(x^2+x-6>0\)
=>\(x^2+3x-2x-6>0\)
=>\(\left(x+3\right)\left(x-2\right)>0\)
TH1: \(\left\{{}\begin{matrix}x+3>0\\x-2>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>2\\x>-3\end{matrix}\right.\)
=>x>2
TH2: \(\left\{{}\begin{matrix}x+3< 0\\x-2< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< -3\\x< 2\end{matrix}\right.\)
=>x<-3
Vậy: TXĐ là \(D=\left(2;+\infty\right)\cup\left(-\infty;-3\right)\)
e: ĐKXĐ: \(x^2-2>0\)
=>\(x^2>2\)
=>\(\left[{}\begin{matrix}x>\sqrt{2}\\x< -\sqrt{2}\end{matrix}\right.\)
Vậy: TXĐ là \(D=\left(-\infty;-\sqrt{2}\right)\cup\left(\sqrt{2};+\infty\right)\)
f: ĐKXĐ: \(\sqrt{x-1}>0\)
=>x-1>0
=>x>1
Vậy: TXĐ là \(D=\left(1;+\infty\right)\)
g: ĐKXĐ: \(x^2+x-6>0\)
=>\(\left(x+3\right)\left(x-2\right)>0\)
=>\(\left[{}\begin{matrix}x>2\\x< -3\end{matrix}\right.\)
Vậy: TXĐ là \(D=\left(2;+\infty\right)\cup\left(-\infty;-3\right)\)

Chọn A
Đk để hàm số xác định là: ![]() . Vậy mệnh đề
. Vậy mệnh đề ![]() đúng.
đúng.
Do hàm số có tập xác định ![]() nên không tồn tại
nên không tồn tại ![]() do đó đồ thị hàm số này không có đường tiệm cận ngang. Vậy mệnh đề
do đó đồ thị hàm số này không có đường tiệm cận ngang. Vậy mệnh đề ![]() sai.
sai.
Do ![]() nên đồ thị hàm số có
nên đồ thị hàm số có ![]() đường tiệm cận đứng là
đường tiệm cận đứng là ![]() và
và ![]() . Vậy
. Vậy ![]() đúng.
đúng.
Ta có
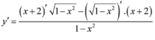
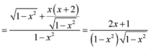
Do ![]() bị đổi dấu qua
bị đổi dấu qua ![]() nên hàm số có một cực trị. Vậy mệnh đề
nên hàm số có một cực trị. Vậy mệnh đề ![]() đúng.
đúng.
Do đó số mệnh đề đúng là ![]() .
.