Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo mình:
để hàm số đồng biến, đk cần là y'=0.
a>0 và \(\Delta'< 0\)
nghịch biến thì a<0
vì denta<0 thì hầm số cùng dấu với a
mình giải được câu a với b
câu c có hai cực trị thì a\(\ne\)0, y'=0, denta>0 (để hàm số có hai nghiệm pb)
câu d dùng viet
câu e mình chưa chắc lắm ^^


Ta có \(y'=-3x^2+6mx\)
Để hàm số đã cho nghịch biến trên \(ℝ\) thì
\(f\left(x\right)=-3x^2+6mx\le0,\forall x\inℝ\)
Thế thì \(\Delta'=9m^2-\left(-3\right).0\le0\) \(\Leftrightarrow m=0\)
Vậy để hàm số đã cho nghịch biến trên \(ℝ\) thì \(m=0\)

\(y'=x^2-2\left(m-2\right)x+m^2-3m+2\)
a. Hàm đồng biến trên khoảng đã cho khi và chỉ khi:
\(y'\ge0\) ; \(\forall x>3\)
\(\Leftrightarrow x^2-2\left(m-2\right)x+m^2-3m+2\ge0\) ; \(\forall x>3\)
Ta có: \(\Delta'=\left(m-2\right)^2-\left(m^2-3m+2\right)=-m+2\)
TH1: \(\Delta'\le0\Leftrightarrow m\ge2\)
TH2: \(\left\{{}\begin{matrix}\Delta'>0\\x_1< x_2\le2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\\left(x_1-2\right)\left(x_2-2\right)\ge0\\\dfrac{x_1+x_2}{2}< 2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\x_1x_2-2\left(x_1+x_2\right)+4\ge0\\x_1+x_2< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m^2-3m+2-4\left(m-2\right)+4\ge0\\2\left(m-2\right)< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m^2-7m+4\ge0\\m< 4\end{matrix}\right.\) \(\Leftrightarrow m< 2\)
Kết hợp lại ta được hàm đồng biến trên \(\left(2;+\infty\right)\) với mọi m
b.
Hàm số đồng biến trên khoảng đã cho khi và chỉ khi:
\(y'\ge0\) ; \(\forall x< 0\)
\(\Leftrightarrow x^2-2\left(m-2\right)x+m^2-3m+2\ge0\) ; \(\forall x< 0\)
TH1: \(\Delta'=-m+2\le0\Leftrightarrow m\ge2\)
TH2: \(\left\{{}\begin{matrix}\Delta'>0\\0\le x_1< x_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\x_1+x_2=2\left(m-2\right)>0\\x_1x_2=m^2-3m+2\ge0\end{matrix}\right.\) \(\Rightarrow\) ko tồn tại m thỏa mãn
Kết hợp lại ta được: \(m\ge2\)

\(y'=3x^2-2\left(2m+1\right)x+m^2+2m=\left(x-m\right)\left(3x-m-2\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}x=m\\x=\dfrac{m+2}{3}\end{matrix}\right.\)
TH1: \(m=\dfrac{m+2}{3}\Rightarrow m=1\) hàm đồng biến trên R (thỏa mãn)
TH2: \(m< \dfrac{m+2}{3}\Rightarrow m< 1\) hàm đồng biến trên khoảng đã cho khi \(\dfrac{m+2}{3}\le0\Rightarrow m\le-2\)
TH3: \(m>\dfrac{m+2}{3}\Rightarrow m>1\) hàm đồng biến trên khoảng đã cho khi \(m\le0\) (ktm)
Vậy \(\left[{}\begin{matrix}m=1\\m\le-2\end{matrix}\right.\)
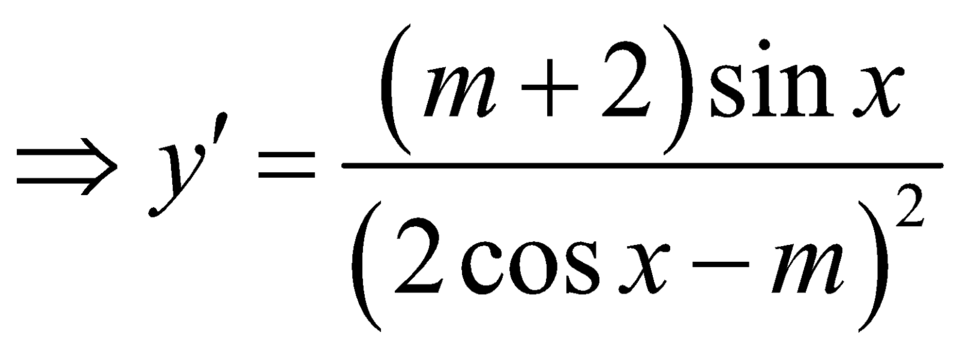 .
.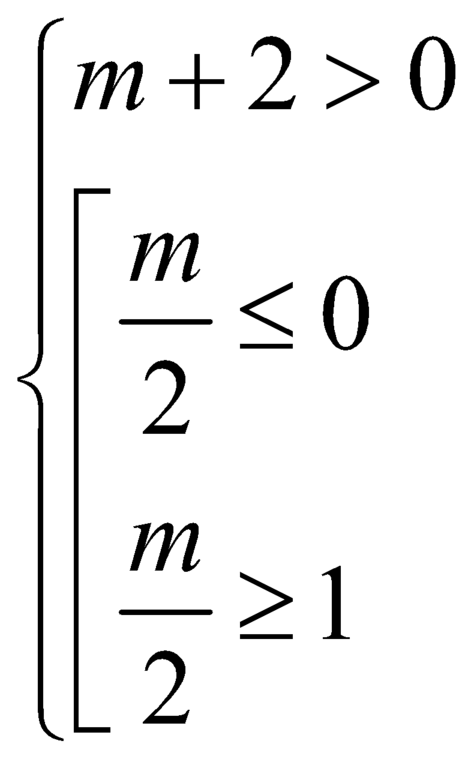
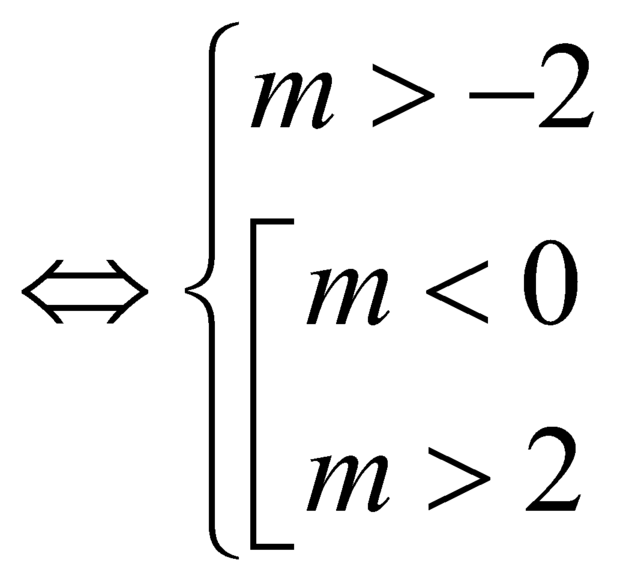

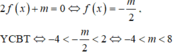


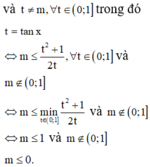
Chọn đáp án A. Có
⇔ m ≤ 0