Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điểm trung bình của xạ thủ A.
|
Giá trị (x) |
Tần số (n) |
Các tích (x.n) |
|
|
8 |
5 |
40 |
|
|
9 |
6 |
54 |
|
|
10 |
9 |
90 |
|
|
|
N = 20 |
Tổng: 184 |
¯¯¯¯¯X=18420=9,2X¯=18420=9,2 |
Điểm trung bình của xạ thủ B.
|
Giá trị (x) |
Tần số (n) |
Các tích (x.n) |
|
|
6 |
2 |
12 |
|
|
7 |
1 |
7 |
|
|
9 |
5 |
45 |
|
|
10 |
12 |
120 |
|
|
|
N = 20 |
Tổng: 184 |
¯¯¯¯¯X=18420=9,2 |
Khả năng của từng người là như nhau
* Điểm trung bình của xạ thủ A
| Giá trị (x) | Tần số (n) | Các tích (x.n) | |
| 8 | 5 | 40 | |
| 9 | 6 | 54 | |
| 10 | 9 | 90 | |
| N = 20 | Tổng: 184 |
X−−− = 184/20 = 9,2 |
* Điểm trung bình của xạ thủ B
| Giá trị (x) | Tần số (n) | Các tích (x.n) | |
| 6 | 2 | 12 | |
| 7 | 1 | 7 | |
| 9 | 5 | 45 | |
| 10 | 12 | 120 | |
| N = 20 | Tổng: 184 |
X−−− = 184/20 = 9,2 |

* Điểm trung bình của xạ thủ A
| Giá trị (x) | Tần số (n) | Các tích (x.n) | |
| 8 | 5 | 40 | |
| 9 | 6 | 54 | |
| 10 | 9 | 90 | |
| N = 20 | Tổng: 184 | X−−− = 184/20 = 9,2 |
* Điểm trung bình của xạ thủ B
| Giá trị (x) | Tần số (n) | Các tích (x.n) | |
| 6 | 2 | 12 | |
| 7 | 1 | 7 | |
| 9 | 5 | 45 | |
| 10 | 12 | 120 | |
| N = 20 | Tổng: 184 | X−−− = 184/20 = 9,2 |

Bảng tần số:
Đối với xạ thủ A

Đối với xạ thủ B

Đáp án cần chọn là: C

TL :
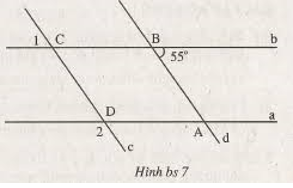
a) Vẽ thêm các tia đối của các tia Dm, Cp, Bq và An.
Vẽ thêm các đường phân giác Ds và Ar của góc ∠D và ∠A.
Khi đó chứng minh được Cp song song với Ds.
Tương tự chứng minh được Ar song song với Dm.
Từ đó suy ra được: An // Cp và Dm // Bq.
b) Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.
Hok tốt

Bài 1:
a)\(\frac{2}{3}.\frac{5}{2}-\frac{3}{4}.\frac{2}{3}=\frac{5}{3}-\frac{1}{2}=\frac{7}{6}\)
b)\(2.\left(\frac{-3}{2}\right)^2-\frac{7}{2}=\frac{2.9}{4}-\frac{7}{2}=\frac{9-7}{2}=\frac{2}{2}=1\)
c)\(-\frac{3}{4}.\frac{68}{13}-0,75.\frac{36}{13}=\frac{-3.4.17}{4.13}-\frac{3.9.4}{4.13}=\frac{-51-27}{13}=\frac{-78}{13}=-6\)
Bài 2:
a)|x-1,4|=1,6
\(\Rightarrow\left[\begin{array}{nghiempt}x-1,4=1,6\\x-1,4=-1,6\end{array}\right.\)
\(\Rightarrow\left[\begin{array}{nghiempt}x=3\\x=-0,2\end{array}\right.\)
b) \(\frac{3}{4}-x=\frac{4}{5}\)
\(x=\frac{3}{4}-\frac{4}{5}=-\frac{1}{20}\)
c)(1-2x)3=-8
(1-2x)3=(-2)3
1-2x=-2
2x=3
x=\(\frac{3}{2}\)
Bài 3:
\(\frac{x}{2}=\frac{y}{5}=\frac{z}{7}=k\)
\(\Rightarrow\begin{cases}x=2k\\y=5k\\z=7k\end{cases}\)
A=\(\frac{2k-5k+7k}{2k+2.5k-7k}=\frac{4k}{5k}=\frac{4}{5}\)
=> x=4/5 . 2= 8/5
y=4/5 . 5=4
z=4/5.7=28/5

















Nhận xét:
+ Xạ thủ B có số lần bắn đạt điểm tối đa (10 điểm) nhiều hơn xạ thủ A (hơn xạ thủ A 3 lần). Tuy nhiên, xạ thủ B cũng có 2 lần bắn chỉ đạt 6 điểm.
+ Trong 20 lần bắn, xạ thủ A đạt được 8 đến 10 điểm, xạ thủ B đạt được 6 đến 10 điểm. Nhìn kết quả có thể thấy xạ thủ A có phong độ ổn định hơn xạ thủ B.
+ Điểm trung bình của hai xạ thủ như nhau nên khả năng của họ là như nhau (9.2 điểm)