Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
+ Sau khi vật B tách rời, vật A dao động với chu kì
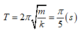
và biên độ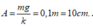 
Khi A lên đến điểm cao nhất thì đi được quãng đường
trong thời gian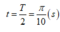 
+ Trong khoảng thời gian t = π/10 (s) vật B rơi tự do được quãng đường
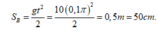
→ khoảng cách giữa hai vật là
Đáp án D
Tại vị trí cân bằng của hệ hai vật ta có
Khi đốt dây, hợp lực tác dụng lên vật A lúc này là:
Lực này gây ra cho vật A gia tốc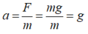 
Vì vật đang ở vị trí biên nên a chính là gia tốc cực đại
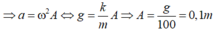
Mà vật A đi từ vị trí thấp nhất đến vị trí cao nhất mất nửa chu kì nên
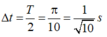
Cũng trong khoảng thời gian ∆ t ấy vật B rơi tự do được quãng đường:
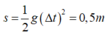
Vậy khoảng cách giữa A và B lúc này là: 2A+1+s=80 cm.
Đáp án A
Hướng dẫn:
Tại vị trí cân bằng O ban đầu lò xo giãn một đoạn Δ l 0 = 2 m g k = 2.1.10 100 = 20 cm.
+ Dây nối bị đứt, vật A sẽ dao động quanh vị trí cân bằng mới O′ nằm trên vị trí cân bằng cũ O một đoạn O ' O = m g k = 1.10 100 = 10 cm.
Tần số góc của dao động ω = k m = 100 1 = 10 rad/s → T = 0,2π s.
→ Tại thời điểm dây bị đứt, vật A có x′ = 10 cm, v′ = 0 → A sẽ dao động với biên độ A = 10 cm.
+ Lần đầu A đạt đến vị trí cao nhất kể từ dây bị đứt ứng với chuyển động của A từ biên dưới đến biên trên → khoảng thời gian tương ứng Δt = 0,5T = 0,1π s.
→ Khoảng cách giữa hai vật:
Δ x = 2 A + l 0 + 1 2 g Δ t 2 = 20 + 10 + 1 2 10 0 , 1 π 2 = 80 cm.
Đáp án C
(Khi cắt đứt dây) =>A=10 cm
Xét ở thời điểm cắt dây đến khi vật lên đến vị trí cao nhất, vật 1 đi được quãng đường S1=20cm
Khi cắt dây thì vật 1 dao động với
Quảng đường vật 2 rơi tụ do trong T/2 (s) là:
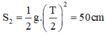
=> Khoảng cách giữa hai vật là:
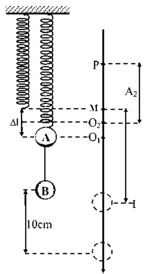
+ Ban đầu, khi hệ 2 vật ở VTCB, lò xo giãn: \(\Delta l_0=\frac{2mg}{k}=\frac{2.1.10}{100}=0,2m=20cm\)
+ Khi đốt sợi dây nối 2 vật, thì còn 1 vật kl m, lúc này vị trí cân bằng mới lò xo giãn: \(\Delta l_{01}=\frac{mg}{k}=0,1m=10cm\)
Như vậy, VTCB mới ở cao hơn VTCB cũ là: 20 - 10 = 10 cm. Và lúc này vật đang từ VTCB cũ mà chuyển động lên, có nghĩa vật cách VTCB mới là 10cm ---> Do vậy, biên độ dao động của vật là 10cm.
+ Chu kì: \(T=2\pi\sqrt{\frac{m}{k}}=2\pi\sqrt{\frac{1}{100}}=0,2\pi s\)
+ Kể từ khi đốt sợi dây, vật lên vị trí cao nhất hết 1/2 chu kì dao động, thời gian là: \(\frac{0,2\pi}{2}=0,1\pi\)s
Khi đó, vật kia rơi tự do đi được quãng đường là: \(S=\frac{1}{2}gt^2=\frac{1}{2}10.\left(0,1\pi\right)^2=0,5m=50cm\)
Khoảng cách giữa 2 vật là: 10 (khoảng cách ban đầu) + 2.10(quãng đường của vật 1 khi đi từ dưới lên vị trí cao nhất) + 50(quãng đường vật 2 rơi)= 80cm.
Đáp án A.
Chọn A
+ Sau khi kéo vật B xuống dưới 20 cm và thả nhẹ thì hệ dao động với biên độ 20cm.
∆l12 = m12g/k = 0,1m = 10cm
Vật B đi lên được h1 = 30 cm thì lực đàn hồi của lò xo triệt tiêu (x12 = -10cm = -A/2). Khi đó vận tốc của B
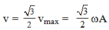
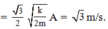
Sau đó vận tốc của vật A có độ lớn giảm dần (vì đang đi về biên trên),
Vật B đi lên thêm được độ cao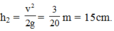
+ Vật B đổi chiều chuyển động khi khi lên được độ cao h = h1 + h2 = 45cm = 0,45m
+ Khoảng thời gian từ khi vậ B tuột khỏi dây nối đến khi rơi đến vị trí thả ban đầu là:
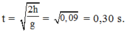
Đáp án A
+ Độ giãn của lò xo tại vị trí cân bằng O của hệ hai vật Δ l 0 = 2 m g k = 5 cm, kéo hệ xuống dưới vị trí cân bằng 10 cm rồi thả nhẹ, vậy hệ sẽ dao động với biên độ A = 10 cm.
+ Ta có thể chia quá trình chuyển động của hệ thành các giai đoạn sau:
Giai đoạn 1: Hệ hai vật dao động điều hòa quanh vị trí cân bằng O.
· Tốc độ của hai vật khi đi qua vị trí cân bằng v m a x = ω A = k 2 m A = 100 2 cm/s.
Giai đoạn 2: Chuyển động của hai vật sau khi đi qua vị trí cân bằng O.
· Khi đi qua vị trí cân bằng O, tốc độ của vật A sẽ giảm, vật B sẽ chuyển động thẳng đứng lên trên với vận tốc ban đầu bằng v m a x , do có sự khác nhau về tốc độ nên hai vật không dao động chung với nhau nữa.
· Tuy nhiên sự kiện trên chỉ diễn ra rất ngắn, vật A ngay sau đó sẽ dao động quanh vị trí cân bằng mới ở phía trên O một đoạn 2,5 cm do đó ngay lập tức tốc độ của A sẽ tăng, trong khi B lại giảm → hệ hai vật lại được xem như ban đầu và dao động quanh vị trí cân bằng O.
Giai đoạn 3: Chuyển động của hai vật sau khi dây bị chùng
· Phương trình định luật II cho vật m 2 : m 2 g − T = m 2 a , khi T = 0 dây chùng → x = − g ω 2 = − 5 cm. Lúc này v A = 3 2 v m a x = 50 6 cm/s.
· Vật dao A dao động quanh vị trí cân bằng mới O' cách vị trí cân bằng cũ một đoạn Δ l = m g k = 2 , 5 cm với biên độ A ' = 2 , 5 2 + 50 6 20 2 = 6 , 61 cm.
Từ các lập luận trên ta thấy rằng khi A dừng lại lần đầu tiên ứng với vị trí biên trên, khi đó quãng đường vật đi được sẽ là S = 10 + 5 + (6,61 – 2,5) = 19,1 cm.
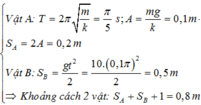
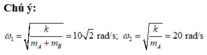
Câu trả lời click vào đây bạn nhé
Đây là một bài tương tự đã được trả lời rùi.