Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Ở hai tam giác bằng nhau yêu cầu các cạnh tương ứng bằng nhau còn ở hai tam giác đồng dạng yêu cầu các cạnh tương ứng có cùng tỉ lê.
- Hai tam giác bằng nhau có ba trường hợp: cạnh góc cạnh, cạnh cạnh cạnh, góc cạnh góc.
- Hai tam giác đồng dạng có ba trường hợp: cạnh góc cạnh, cạnh cạnh cạnh, góc góc.

- Có
- Các trường hợp là :
đồng dạng (c.c.c) , đồng dạng (g.g) , đông dạng (c.g.c)
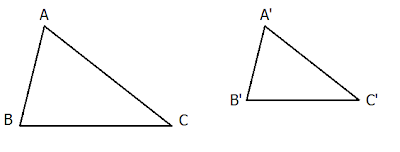
Tam giác đồng dạng có hai tính chất quan trọng sau đây: Ba cặp góc bằng nhau∠A=∠A′, ∠B=∠B′, ∠C=∠C′
Ba cặp cạnh tỉ lệ với nhauABA′B′=BCB′C′=CAC′A′
đồng dạng (c.c.c) , đồng dạng (g.g) , đồng dạng (c.g.c)

Tam giác đồng dạng có hai tính chất quan trọng sau đây: Ba cặp góc bằng nhau∠A=∠A′, ∠B=∠B′, ∠C=∠C′
Ba cặp cạnh tỉ lệ với nhauABA′B′=BCB′C′=CAC′A′
Vậy làm thế nào để chứng minh hai tam giác là đồng dạng với nhau. Thông thường chúng ta có ba cách sau đây.
Trường hợp Góc - Góc: hai tam giác có hai cặp góc bằng nhau là hai tam giác đồng dạng với nhau
Ở hình dưới đây, nếu chúng ta chỉ ra được∠A=∠A′ và ∠B=∠B′thì chúng ta có thể kết luận rằng hai tam giác ABC và A′B′C′ là đồng dạng với nhau.

Trường hợp Cạnh - Cạnh - Cạnh: hai tam giác có ba cặp cạnh tỉ lệ với nhau là hai tam giác đồng dạng với nhau
Ở hình dưới đây, nếu chúng ta chỉ ra đượcABA′B′=BCB′C′=CAC′A′
thì chúng ta có thể kết luận rằng hai tam giác ABC và A′B′C′ là đồng dạng với nhau.

Trường hợp Cạnh - Góc - Cạnh: hai tam giác có hai cặp cạnh tỉ lệ với nhau và cặp góc xen giữa hai cặp cạnh này bằng nhau thì đó là hai tam giác đồng dạng với nhau
Ở hình dưới đây, nếu chúng ta chỉ ra đượcABA′B′= BCB′C′ và ∠B=∠B′thì chúng ta có thể kết luận rằng hai tam giác ABC và A′B′C′ là đồng dạng với nhau.

- Nếu hai tam giác là hai tam giác vuông thì việc chứng minh hai tam giác là đồng dạng còn đơn giản hơn nữa. Chúng ta có các cách sau đây.
Trường hợp Góc Nhọn: hai tam giác vuông có một cặp góc nhọn bằng nhau là hai tam giác đồng dạng với nhau
Ở hình dưới đây, nếu chúng ta chỉ ra được∠A=∠A′thì chúng ta có thể kết luận rằng hai tam giác vuông ABC và A′B′C′ là đồng dạng với nhau.

Trường hợp Cạnh - Cạnh: hai tam giác vuông có hai cặp cạnh tỉ lệ với nhau là hai tam giác đồng dạng với nhau
Ở hình trên đây, nếu chúng ta chỉ ra đượcABA′B′= BCB′C′, hoặc BCB′C′= CAC′A′, hoặc CAC′A′= ABA′B′thì chúng ta có thể kết luận rằng hai tam giác vuông ABC và A′B′C′ là đồng dạng với nhau.

a) Mệnh đề Đúng.
Giả sử có ΔABC = ΔA’B’C’
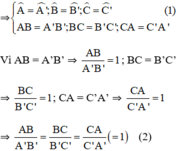
Từ (1) và (2) suy ra 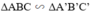
b) Mệnh đề Sai.
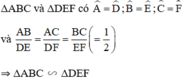
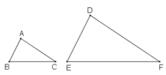
nhưng ΔABC và ΔDEF không bằng nhau

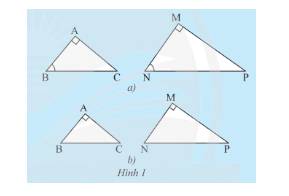
a) Xét tam giác \(ABC\) và tam giác \(MNP\) ta có:
\(\widehat B = \widehat N\) (giả thuyết)
\(\widehat A = \widehat M = 90^\circ \).
Do đó, \(\Delta ABC\backsim\Delta MNP\) (g.g)
b) Xét tam giác \(ABC\) và tam giác \(MNP\) ta có:
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}\) (giả thuyết)
\(\widehat A = \widehat M = 90^\circ \).
Do đó, \(\Delta ABC\backsim\Delta MNP\) (c.g.c).

Gọi x là số học sinh (tần số) được điểm 5 (x ∈ N; 0 ≤ x ≤ 4).
Tần số hay số học sinh được điểm 9 là:
10 – (1 + 2 + 3 + x) = 4 – x
Điểm trung bình của cả tổ bằng 6,6 điểm nên:





Trường hợp
Đúng
Sai
a. 1,5cm, 2cm, 3cm và 4,5cm, 6cm, 9cm.
x
b. 2,5cm, 4cm, 5cm và 5cm, 12cm, 8cm.
x
c. 3,5cm, 6cm, 7cm và 15cm, 12cm, 7cm.
x
d. 2cm, 5cm, 6,5cm và 13cm, 10cm, 4cm.
x