Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: C
Hệ hai quả cầu là một hệ cô lập về điện. Theo định luật bảo toàn điện tích, tổng đại số của các điện tích của hai quả cầu không đổi. Mặt khác điện tích
q
1
dương,
q
2
âm và độ lớn của điện tích
q
1
lớn hơn điện tích
q
2
nên sau khi hai quả tiếp xúc nhau rồi tách chúng ra thì hai quả cầu cùng mang điện tích dương, có cùng độ lớn là: 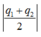

Đáp án C
Hệ hai quả cầu là một hệ cô lập về điện. Theo định luật bảo toàn điện tích, tổng đại số của các điện tích của hai quả cầu không đổi. Mặt khác điện tích q 1 dương, q 2 âm và độ lớn của điện tích q 1 lớn hơn điện tích q 2 nên sau khi hai quả tiếp xúc nhau rồi tách chúng ra thì hai quả cầu cùng mang điện tích dương, có cùng độ lớn là
q 1 + q 2 2

Đáp án C
Hệ hai quả cầu là một hệ cô lập về điện. Theo định luật bảo toàn điện tích, tổng đại số của các điện tích của hai quả cầu không đổi. Mặt khác điện tích q 1 dương, q 2 âm và độ lớn của điện tích q1 lớn hơn điện tích q 2 nên sau khi hai quả tiếp xúc nhau rồi tách chúng ra thì hai quả cầu cùng mang điện tích dương, có cùng độ lớn là q 1 + q 2 2


Sau khi cho hai quả cầu tiếp xúc với nhau thì mỗi quả cầu sẽ mang điện tích:
\(q'=\dfrac{q+0}{2}=\dfrac{q}{2}\)
Lực tương tác giữa hai quả cầu là lực điện: \(F=k.\dfrac{\left|q'\right|.\left|q'\right|}{r^2}=k.\dfrac{\left(\dfrac{q}{2}\right)^2}{2.sin\alpha.l}=k.\dfrac{\left(\dfrac{q}{2}\right)^2}{2.sin30^0}=k\left(\dfrac{q}{2}\right)^2\)
Xét một trong hai quả cầu (giả sử quả cầu nằm bên trái), ta có:
\(tan\alpha=\dfrac{F}{P}=\dfrac{k\left(\dfrac{q}{2}\right)^2}{mg}\)
\(\Rightarrow\left|q\right|=2\sqrt{\dfrac{tan\alpha.mg}{k}}=2\sqrt{\dfrac{tan30^0.5.10^{-3}.10}{9.10^9}}=3,58.10^{-6}C\)

Gọi q1,q2 là điện tích của quả cầu 1 và quả cầu 2 trước khi chúng tiếp xúc với nhau.Độ lớn của lực tương tác giữa chúng được xác định theo định luật Culông :
\(F_1=k\frac{\left|q_1q_2\right|}{r^2}\) từ đó \(q_1q_2=-\frac{F_1r^2}{k}\) (có dấu \(\text{"−"}\) vì hai điên tích \(q_1,q_2\) trái dấu)
Thay số ta được : \(q_1q_2=-\frac{6,4}{9}.10^{-13}\left(1\right)\)
Sau khi tiếp xúc với nhau, điện tích của hai quả cầu trở nên bằng nhau và có độ lớn bằng \(\frac{\left|q_1+q_2\right|}{2}\) do đó lực đẩy giữa chúng là: \(F_2=\frac{k\left(\frac{q_1+q_2}{2}\right)^2}{r^2}\)
Suy ra \(\left(q_1+q_2\right)^2=\frac{4F_2r^2}{k}\) Thay số vào ta được \(\left(q_1+q_2\right)^2=16.10^{-14}\)
hay : \(q_1+q_2=\pm4.10^{-7}\left(2\right)\)
Giải hệ phương trình (1),(2) ta được :
\(q_1=-\frac{4}{3}.10^{-7}\approx-1,33.10^{-7}C\)
\(q_2=\frac{16}{3}.10^{-7}\approx5,33.10^{-7}C\)
hoặc \(q_1=\frac{4}{3}.10^{-7}\approx1,33.10^{-7}C\)
\(q_2=-\frac{16}{3}.10^{-7}\approx-5,33.10^{-7}C\)
Đáp án cần chọn là: C